在之前的Q-table中,由于Q值与感知态的强绑定问题,无法学习随机策略(也无法区分感知相同但需求不同的状态,比如说非对称),因此需要使用PG求解,
在一些情节,比如说机器臂(连续动作空间),石头剪刀布(概率性策略)中,我们可以使用PG,同时,��收敛性也更加强
PG的主要目的就是计算梯度并更新参数来改变策略,直接输出动作概率
1. 理论
首先给出轨迹的概念,把环境输出的s与演员输出的动作a全部组合起来,就是一个轨迹(trajectory)
τ=s1,a1,s2,a2,...,st,at
就像是神经网络一样,前输出就是后输入
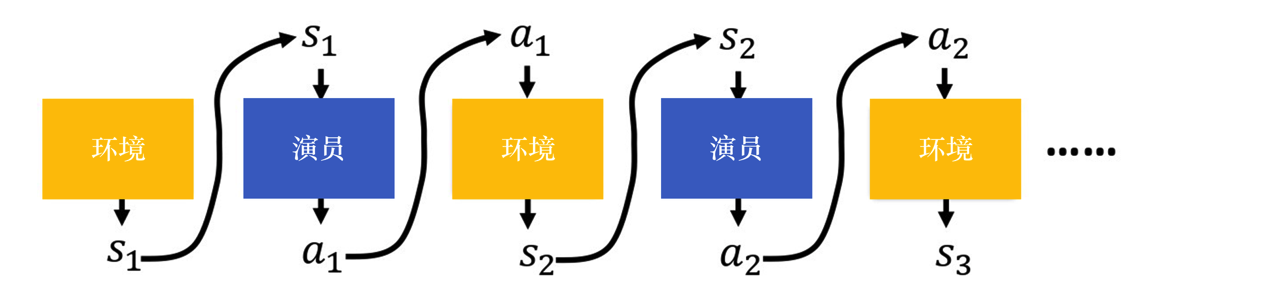
在给定参数θ,计算某个轨迹τ发生的概率为
pθ(τ)=p(s1)pθ(a1∣s1)p(s2∣s1,a1)pθ(a2∣s2)p(s2∣s1,a1)⋯=p(s1)t=1∏Tpθ(at∣st)p(st+1∣st,at)
其中,p(s1)为厨师状态分布(也就是起点),pθ(at∣st)为策略在状态st下选择动作at的概率,p(st+1∣st,at)为状态转移概率
一句话概括一下的话,就是在给定策略πθ(或pθ)下,一整条轨迹τ出现的概率是多少。这公式蛮重要的,是后续梯度下降的基础。就是上图的数学表达而已,不复杂
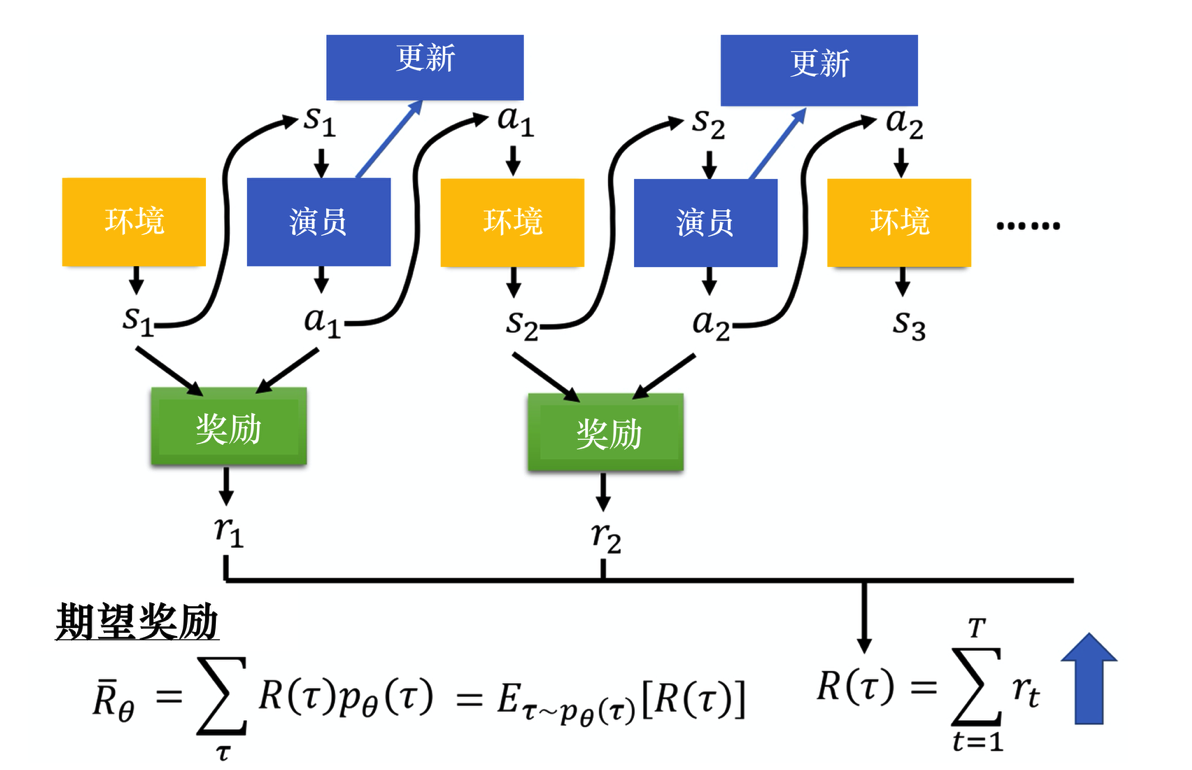 改图是计算奖励的过程,R(τ)就是每个步骤获取的奖励累加,
改图是计算奖励的过程,R(τ)就是每个步骤获取的奖励累加,
在某一场游戏的某一个回合里面,我们会得到R(τ)。我们要做的就是调整演员内部的参数θ, 使得R(τ)的值越大越好。 但实际上R(τ)并不只是一个标量(scalar),它是一个随机变量,因为演员在给定同样的状态下会采取什么样的动作,这是有随机性的。环境在给定同样的观测时要采取什么样的动作,要产生什么样的观测,本身也是有随机性的,所以R(τ)是一个随机变量。我们能够计算的是R(τ)的期望值。给定某一组参数,我们可计算rθ的期望值为
Rˉθ=τ∑R(τ)pθ(τ)
比如θ对应的模型很强,如果有一个回合θ很快就死掉了,因为这种情况很少会发生,所以该回合对应的轨迹τ的概率就很小;如果有一个回合一θ直没死,因为这种情况很可能发生,所以该回合对应的轨迹τ的概率就很大。我们可以根据θ算出某一个轨迹τ出现的概率,接下来计算τ的总奖励。总奖励使用τ出现的概率进行加权,对所有的τ进行求和,就是期望值。给定一个参数,我们可以计算期望值为
Rˉθ=Eτ∼pθ(τ)[R(τ)]
这就引入正文主题了,想让奖励越大越好,就需要梯度,而且是上升来最大化期望奖励,即
∇Rˉθ=τ∑R(τ)∇pθ(τ)
不过,由于期望无法直接求导,会用一大堆公式进行推导,得到可以通过采样计算的梯度。数学技巧使用的是∇f(x)=f(x)∇logf(x).推导公式不放了,感兴趣自己去搜,网上都有,最终公式是这样的,这是梯度的近似计算方法
N1n−1∑Nt=1∑TnR(τn)∇logpθ(atn∣stn)
也很复杂,不看,给出最简单的形式,用于更新θ
θ←θ+η∇Rˉθ
其中,η是学习率,可用Adam等深度学习里的方法来进行调整
注意,一般**策略梯度(policy gradient,PG)**采样的数据只会用一次。我们采样这些数据,然后用这些数据更新参数,再丢掉这些数据。接着重新采样数据,才能去更新参数。
2. 策略梯度实现技巧
2.1 添加基线(baseline)
在很多环境中,奖励R(τ)永远是正数(例如迷宫中只要活着就给分)。根据基础公式,只要我们采样到了某个动作,它的概率就会增加。如果某些好的动作没被采样到,它们的相对概率反而会下降,这显然不合理。
解决方法:��给奖励减去一个基线 b(通常是所有奖励的平均值)
只有比“平均水平”更好的动作,奖励才会是正的(增加概率);比平均水平差的动作,奖励会变成负的(降低概率)。
2.2 指派合适的分数 (Assign Suitable Credit)
在基础算法中,每一局游戏(轨迹τ)得到的总奖励R(τ)会被乘到该局的每一个动作上。但这不公平——也许你开局走得非常好,但最后一步失误导致输了。在基础公式里,开局的那个“好动作”也会被惩罚。
解决方法:不再使用整场游戏的总分,而是使用该动��作之后产生的累积奖励,即用Gt代替R(τ)
目的是一个动作的评价,只取决于它做完之后发生的奖励。这大大减少了评价中的“噪音”,让梯度更新更准确。
2.3 总结
看一下了解一下就行,2.2是一个经典的评论员(critic)。后续会专门再写一个评价员算法
3. REINFORCE:蒙特卡洛策略梯度(Monte Carlo Policy Gradient)
REINFORCE 用的是回合更新的方式,它在代码上的处理上是先获取每个步骤的奖励,然后计算每个步骤的未来总奖励Gt,将每个Gt代入
∇Rˉθ≈N1n=1∑Nt=1∑TnGtn∇logπθ(atn∣stn)
Gt需要从后往前算,逐步推导到G1,具体表现为
Gt=k=t+1∑Tγk−t−1rk=rt+1+γGt+1
即上一个步骤和下一个步骤的未来总奖励的关系,其实就是原本是(s,a)现在变成了(s,a,G),即
(s1,a1,G1)(s2,a2,G2),...,(sT,aT,GT)
 改图是计算奖励的过程,就是每个步骤获取的奖励累加,
改图是计算奖励的过程,就是每个步骤获取的奖励累加,