FEMATHS 学习小组的故事可以追溯到 2023 年 6 月。当时，JoyBun、zqqqqqqj1110 和 Tanger 三人决定一起攻读与 PINN（Physics-Informed Neural Networks）相关的论文，以突破各自在学习中遇到的瓶颈。

但在阅读过程中，大家逐渐意识到：不仅 JoyBun 和 zqqqqqqj1110 对 PINN 感到困惑，连相对熟悉一些的 Tanger 也有许多难以理解的地方。于是我们决定边读论文边做笔记。虽然这些笔记可能显得 粗浅、幼稚，甚至不乏理解上的偏差，但我们仍希望将它们整理出来。我们相信，通过写笔记的方式，可以尽可能清晰地梳理出 PINN 以及人工智能相关论文中的核心思想和原理。我们希望用最朴素的学习方法，把复杂的内容讲明白——用简单的努力，积累不平凡的价值。

这，就是 FEMATHS 小组学习日志 的由来。

后来，随着 Tanger 面临考研与工作的压力，科研学习和小组学习日志一度中断。直到 2025 年，桂林电子科技大学数学与计算科学学院公布拟录取名单，Tanger 顺利被录取。这也成为重新启动学习日志的契机——新的笔记就此续写。

科技论文是学者与研究人员进行学术交流的重要方式。通过阅读科技论文，不仅可以了解当前领域的研究进展，还能提升自己对复杂问题的认知能力和理解力。在学习过程中，书籍 📕、网站 🖥、期刊论文等都是常见且有效的起点资源。

🔍 如何找到一篇合适的科技论文​

在上一节中，我们已经了解了科技论文的基本结构及其产生过程，相信你对科技论文已有初步认识。接下来，我们将学习如何寻找一篇适合阅读的科技论文。

找到一篇合适的论文，对于入门新领域、拓展知识视野具有重要意义。一篇好的论文能够帮助你：

• 快速了解某个研究方向的基本概念；
• 把握领域内的研究重点与热点问题；
• 学习论文写作的结构与逻辑表达方式。

这是一篇使用 VPinn 来求解 Navier-Stokes 方程的论文。

我们先来看看这篇论文的摘要：

摘要​

英文原文：

We present TSA-PINN, a novel Physics-Informed Neural Network (PINN) that leverages a Trainable Sinusoidal Activation (TSA) mechanism to approximate solutions to the Navier-Stokes equations. By incorporating neuronwise sinusoidal activation functions with trainable frequencies and a dynamic slope recovery mechanism, TSAPINN achieves superior accuracy and convergence. Its ability to dynamically adjust activation frequencies enables efficient modeling of complex fluid behaviors, reducing training time and computational cost. Our testing goes beyond canonical problems, to study less-explored and more challenging scenarios, which have typically posed difficulties for prior models. Various numerical tests underscore the efficacy of the TSA-PINN model across five different scenarios. These include steady-state two-dimensional flows in a lid-driven cavity at two different Reynolds numbers; a cylinder wake problem characterized by oscillatory fluid behavior; and two time-dependent three-dimensional turbulent flow cases. In the turbulent cases, the focus is on detailed near-wall phenomenaincluding the viscous sub-layer, buffer layer, and log-law region—as well as the complex interactions among eddies of various scales. Both numerical and quantitative analyses demonstrate that TSA-PINN offers substantial improvements over conventional PINN models. This research advances physics-informed machine learning, setting a new benchmark for modeling dynamic systems in scientific computing and engineering.

翻译：

我们介绍 TSA-PINN，一种新型物理知情神经网络（PINN），利用可训练正弦激活（TSA）机制近似纳维-斯托克斯方程的解。通过结合具有可训练频率的神经元正弦激活功能和动态斜坡恢复机制，TSAPINN 实现了卓越的准确性和收敛性。其动态调节激活频率的能力使复杂流体行为的高效建模成为可能，从而缩短训练时间和计算成本。我们的测试超越了典型问题，还研究了较少被探索且更具挑战性的情景，这些通常对以往模型来说是困难。各种数值测试强调了 TSA-PINN 模型在五种不同情景中的有效性。这些包括在两个不同雷诺数下，盖子驱动腔内的稳态二维流动;一个以振荡流体行为为特征的圆柱尾流问题;以及两个时间相关的三维湍流情况。湍流情况下，重点关注详细的近壁现象，包括粘性亚层、缓冲层和对数定律区域——以及不同尺度涡流之间的复杂相互作用。数值和定量分析均表明，TSA-PINN 相较传统 PINN 模型有显著改进。这项研究推动了基于物理的机器学习，为科学计算和工程中动态系统建模树立了新标杆。

1.1 概述​

懒的说了，自己百度一下什么都有，或者去看AI世界大入门去

1 马尔可夫性质(Markov property)​

对于天气预报而言，今天是否下雨只取决于前一天的天气情况，无关于前2345...n天的情况。这就是MP(马尔可夫性质，下文简称MP)

换句话来说，一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。给出公式如下

此处假设随机变量$X_0, X_1, ..., X_T$为一个随机过程。公式代表的含义指需要看每个p的后半部分**(｜xxx)**，意思就是前面的都不用看，看个t就行。

MP也可以描述为给定当前状态时，将来的状态与过去状态是条件独立的。如果某一个过程满足马尔可夫性质，那么未来的转移与过去的是独立的，它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。

策略最简单的表示是查找表（look-up table），即表格型策略（tabular policy）。使用查找表的强化学习方法称为表格型方法（tabular method），如蒙特卡洛、Q学习和Sarsa。本章通过最简单的表格型方法来讲解如何使用基于价值的方法求解强化学习问题。（reference：https://datawhalechina.github.io/easy-rl/#/chapter3/chapter3）

基于此，本文介绍三种常用方法，Q表格（Q-table）， 时序差分（temporal difference），蒙特卡洛（MC），Sarsa

并稍微给出免模型，有模型，同策略，异策略的定义

1 免模型 (Model-free) 和 有模型 (Model-based)​

1.1 Model-free​

直接与环境互动，不考虑环境内的数学公式，特点是通过反复试错来改进策略，但是模拟次数需要很多

当马尔可夫决策过程的模型未知或者模型很大时，我们可以使用免模型强化学习的方法。免模型强化学习方法没有获取环境的状态转移和奖励函数，而是让智能体与环境进行交互，采集大量的轨迹数据，智能体从轨迹中获取信息来改进策略，从而获得更多的奖励。

1.2 model-based​

先构建虚拟环境，在其中训练后在将模型放在真实环境中执行，特点是学习速度快（虚拟环境可以理解为概率论中的先验知识），但是极度依赖模型的准确性

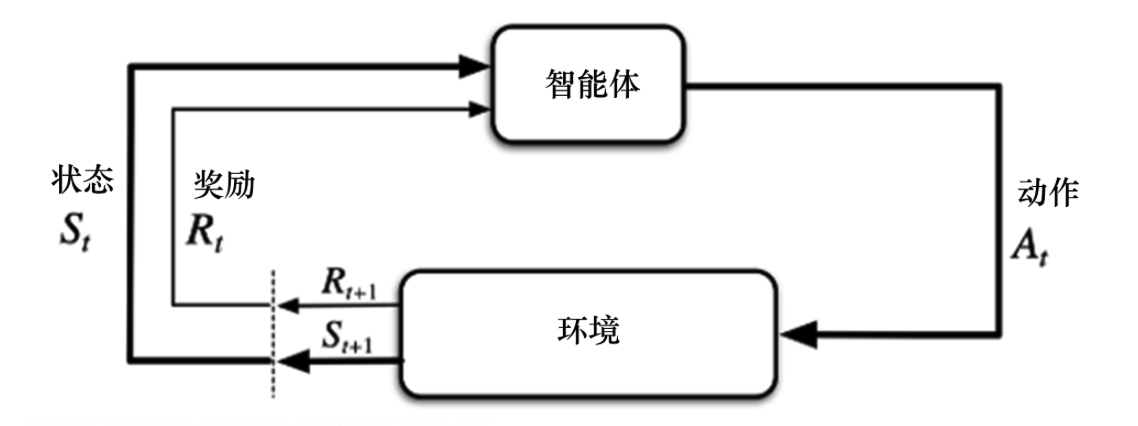
策略迭代和价值迭代都需要得到环境的转移和奖励函数，所以在这个过程中，智能体没有与环境进行交互。在很多实际的问题中，马尔可夫决策过程的模型有可能是未知的，也有可能因模型太大不能进行迭代的计算，比如雅达利游戏、围棋、控制直升飞机、股票交易等问题，这些问题的状态转移非常复杂。

2 Q表格​

Q表格可以这样理解，在一个5*5的网格中，每一个网格都会记录最佳策略，当agent走到这步的时候，就可以直接通过查表的方式去决定自己的策略。其实和动态规划的思想差不多。baseline如下

q值代表在某个状态下采取某个动作，未来预期能获得的累积奖励总和。初始化一般都可以默认为0

Q表格很好用，但是action和state很多都情况下就太大了，这就是未来会介绍到的DQN算法。当然，本文不介绍，而是介绍几种常见的计算q_value的办法

当然在此之前，我们还需要了解一下同策略和异策略

3 同策略(on-policy) & 异策略(off-policy)​

本文介绍三种算法，简单说就是蒙特卡洛方法 (Monte Carlo, MC)，时序差分方法 (Temporal Difference, TD)和SARSA。其中Q-learning和SARSA都是TD的具体实现方法

4 蒙特卡洛策略评估(Monte Carlo, MC)​

4.1 理论​

一句话，**就是大数仿真模拟然后求平均值。**采样大量的轨迹，计算所有轨迹的真实回报，然后计算平均值。

让agent先完整的完成一个回合，然后记录下从某个状态开始到结束所拿到的所有奖励

算法流程

1. 采样：从状态s采取动作a开始，直到结束或epochs用完
2. 计算$G_t$: 计算回报
3. 更新表格的Q_value：有两种形式

第一个很简单，直接平均就ok了，第二个是增量更新法，也是最常用的一种办法，

$\alpha$是学习率，$(G_t - Q(s,a)$是误差，决定其收敛，大于0说明鼓励这个动作，小于0说明惩罚这个动作

4.2 例子​

4.2.1 设定​

假设存在这样的一个迷宫

Reward：到达终点+10，陷阱-10，移动一步-1

$\gamma = 1, \alpha=0.5$,使用增量更新法，init all q_value in Q table are 0

4.2.2 计算​

只模拟三步

如果是Q table的话，就是这样的

如果遇见一个坐标是之前计算过的，务必不要忘记使用增量更新法

5 时序差分（Temporal Difference, TD）​

依旧是一种填表的方法，不同的是TD不需要等一局结束（不需要注意$G_t$）每走n不就更新一次Q表（也就是TD(n)）

5.1 TD(0)​

5.1.1 理论​

以最简单的TD（0）为例，核心公式为

$V(s_t)$为目前（最好的翻译是以前）这个格子的分数（旧预测），$r_{t+1} + \gamma V(s_{t+1})-V(s_t)$就是TD目标（TD target）

**时序差分误差（TD error）**就是$\delta = R_{s'} + \gamma V(s') - V(s)$,可以用更新$V(s)$来逼近真实的回报

5.1.2 例子​

还是以迷宫为例，只不过这次初始化的是V Table

V值在确定TD error的情况下，可以直接简化计算，即$V(s_t) = V(s_t) + \gamma \delta$

此处还需要引入一个重要概念，V表是有局限性的，尤其是针对model-free的情况，因为V表没有动作a，意思就是不知道应该如何计算状态转移概率$p(s_{t+1}|s_t,a)$，所以这不是一种Q-Table的传统算法。当然，后续的Q-learning和SARSA就是两种计算V表然后再计算Q表的算法了

6. 广义策略迭代 (Generalized Policy Iteration, GPI)​

为什么需要广义策略迭代？因为在不知道$P(s' \mid s, a)$和$R(s, a)$的情况下，即便算出了$V(s)$,也无法推导出最优动作，（公式如下，方便理解）

此时就需要使用到GPI，广义策略迭代是指策略评估 (Policy Evaluation)和策略改进 (Policy Improvement)这两个过程相互作用、不断迭代的过程。

Evaluation根据当前策略$\pi$来估算价值函数（$V$或$Q$）

Improvement是指，得到价值函数后，通过“贪心”的方法改进策略，使其朝着更优的方向演变

对策略评估部分进行修改，使用蒙特卡洛的方法代替动态规划的方法估计 Q 函数。我们首先进行策略评估，使用蒙特卡洛方法来估计策略$Q=Q_\pi$，然后进行策略更新，即得到 Q 函数后，我们就可以通过贪心的方法去改进它

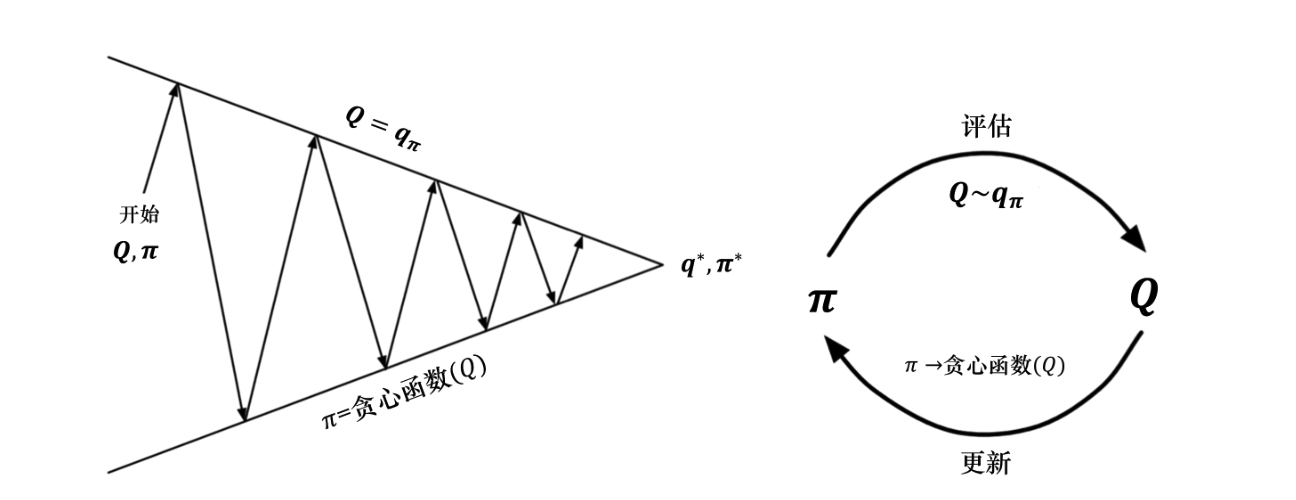
最好的该改进点是，在之前，只要不知道P和R，求出V也没用。但现在可以直接评估Q函数（通过Q表），直接选取Q值最大的动作

有两种方案：

A：MC探索

B：e-贪心搜索

6. SARSA​

6.1 理论​

先说定义：Sarsa 是一种**同策略（on-policy）**算法，它优化的是它实际执行的策略，它直接用下一步会执行的动作去优化 Q 表格。同策略在学习的过程中，只存在一种策略，它用一种策略去做动作的选取，也用一种策略去做优化。所以 Sarsa 知道它下一步的动作有可能会跑到悬崖那边去，它就会在优化自己的策略的时候，尽可能离悬崖远一点。这样子就会保证，它下一步哪怕是有随机动作，它也还是在安全区域内。

SARSA不同于前文讲的那些，是直接作用于$Q(s,a)$的，其计算公式为

是不是很想前文的TD？这就是照搬了思路而已，当然该公式只是策略评估，对于策略改进，我们需要使用$\epsilon-greedy$

6.2 例子​

依旧迷宫，当然此处假设$\epsilon=0.1$（90%选分最高的，10%瞎跑）

Step1（s） 策略改进（决定这么走）

从s1出发，应该附近都是0，所以通过$\epsilon-greedy$随机选择了一个动作向右，此时的状态动作为(s1, 右边)

Step2（a，r） 执行与观测

agent往右走并进入了空地s2，获取了奖励$r=-1$

Step3（s‘） 再次策略改进（SARSA）

在更新s1的分数之前，先决定在s2应该怎么走，发现目前Q表也是0，于是通过$\epsilon-greedy$决定向下走

Step4（a’，Q）策略评估

利用前几步，带入公式

此时更新好了全新的$Q(s_1, 右)$，依旧进行n轮迭代得到最终解

6.3 总结​

用TD的方法（计算Q）+$\epsilon-greedy$更新策略，就得到了SARSA，这个算法的本身就是$s,a,r,s',a'$

7. Q学习（Q-learning）​

7.1 理论​

和SARSA差不多，只是稍微变了一下Q值更新策略，首先列出公式

TD target发生了变化

7.2 实验​

和SARSA一样，不同点在于step4，更新评估部分

$\epsilon-greedy$在确定动作之后，比如$(s_2, 左)$,SARSA就会用$(s_2, 左)$的值带入公式计算新Q值，而Q-learning会不管$\epsilon-greedy$的结果，直接选择附近的最高Q值，即在填表时只选最高的走，以追求最优解

8. 同策略与异策略​

Sarsa 是一个典型的同策略算法，它只用了一个策略$\pi$，它不仅使用策略$\pi$学习，还使用策略$\pi$与环境交互产生经验。 如果策略采用$\epsilon-greedy$，它需要兼顾探索，为了兼顾探索和利用，它训练的时候会显得有点“胆小”。它在解决悬崖行走问题的时候，会尽可能地远离悬崖边，确保哪怕自己不小心探索了一点儿，也还是在安全区域内。此外，因为采用的是，$\epsilon-greedy$策略会不断改变（$\epsilon$值会不断变小），所以策略不稳定。

Q学习是一个典型的异策略算法，它有两种策略————目标策略和行为策略，它分离了目标策略与行为策略。Q学习可以大胆地用行为策略探索得到的经验轨迹来优化目标策略，从而更有可能探索到最佳策略。行为策略可以采用 εε-贪心 算法，但目标策略采用的是贪心算法，它直接根据行为策略采集到的数据来采用最佳策略，所以 Q学习 不需要兼顾探索。

我们比较一下 Q学习 和 Sarsa 的更新公式，就可以发现 Sarsa 并没有选取最大值的最大化操作。因此，Q学习是一个非常激进的方法，它希望每一步都获得最大的利益；Sarsa 则相对较为保守，它会选择一条相对安全的迭代路线。

总结

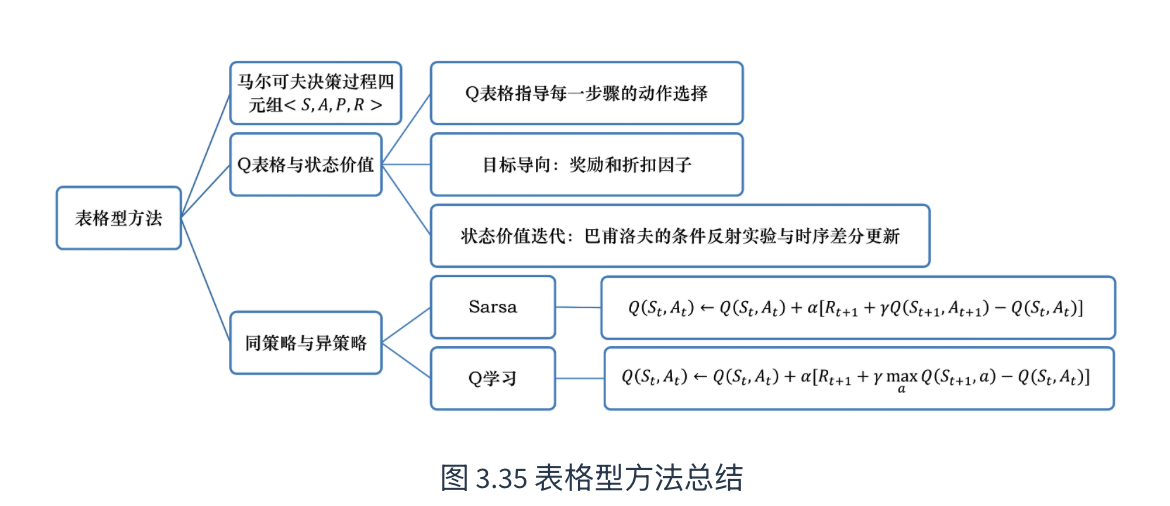
8. 一些定义​

**自举（Bootstrapping）**是指在更新当前状态或动作的价值时，不等待最终的真实回报，而是直接利用对后续状态价值的“现有估计值”来更新当前的“估计值”

在之前的Q-table中，由于Q值与感知态的强绑定问题，无法学习随机策略（也无法区分感知相同但需求不同的状态，比如说非对称），因此需要使用PG求解，

在一些情节，比如说机器臂（连续动作空间），石头剪刀布（概率性策略）中，我们可以使用PG，同时，收敛性也更加强

PG的主要目的就是计算梯度并更新参数来改变策略，直接输出动作概率

1. 理论​

首先给出轨迹的概念，把环境输出的$s$与演员输出的动作$a$全部组合起来，就是一个轨迹(trajectory)

就像是神经网络一样，前输出就是后输入

在给定参数$\theta$，计算某个轨迹$\tau$发生的概率为

其中，$p(s_1)$为厨师状态分布（也就是起点），$p_{\theta}(a_t \mid s_t)$为策略在状态$s_t$下选择动作$a_t$的概率，$p(s_{t+1} \mid s_t, a_t)$为状态转移概率

一句话概括一下的话，就是在给定策略$\pi_{\theta}$（或$p_{\theta}$）下，一整条轨迹$\tau$出现的概率是多少。这公式蛮重要的，是后续梯度下降的基础。就是上图的数学表达而已，不复杂

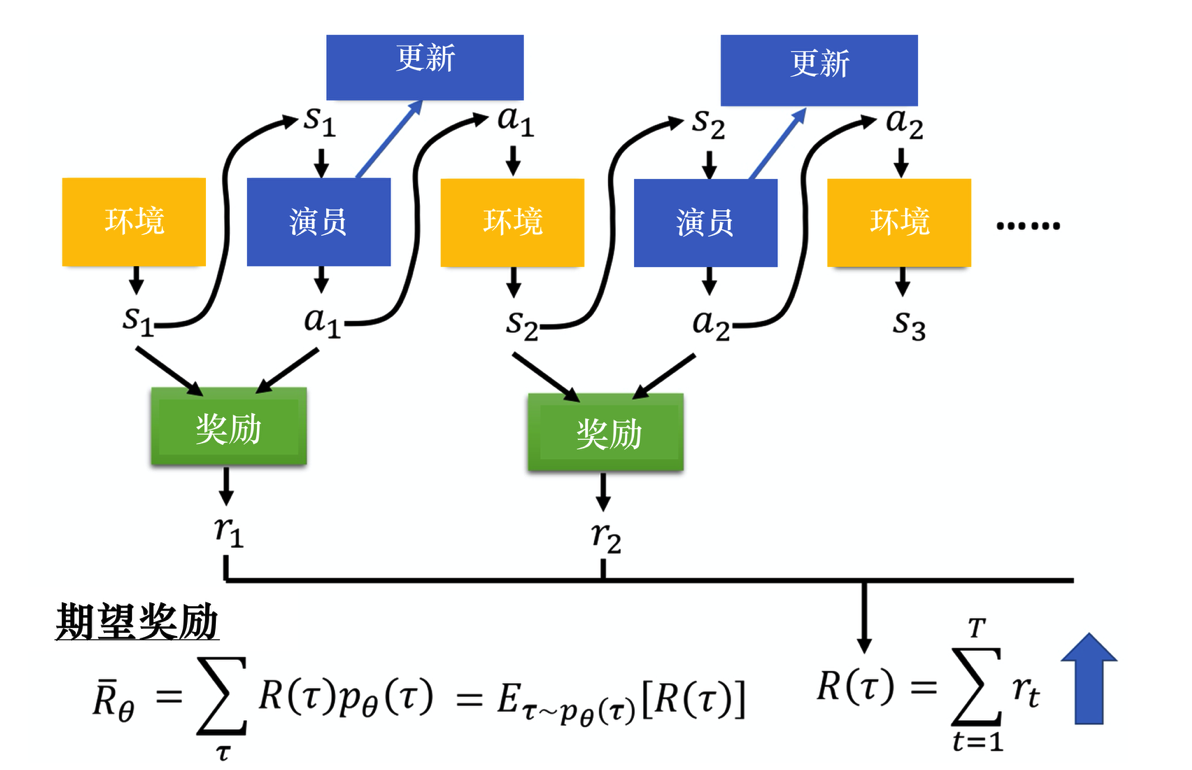改图是计算奖励的过程，$R(\tau)$就是每个步骤获取的奖励累加，

在某一场游戏的某一个回合里面，我们会得到$R(\tau)$。我们要做的就是调整演员内部的参数$\theta$， 使得$R(\tau)$的值越大越好。 但实际上$R(\tau)$并不只是一个标量（scalar），它是一个随机变量，因为演员在给定同样的状态下会采取什么样的动作，这是有随机性的。环境在给定同样的观测时要采取什么样的动作，要产生什么样的观测，本身也是有随机性的，所以$R(\tau)$是一个随机变量。我们能够计算的是$R(\tau)$的期望值。给定某一组参数，我们可计算$r_\theta$的期望值为

比如$\theta$对应的模型很强，如果有一个回合$\theta$很快就死掉了，因为这种情况很少会发生，所以该回合对应的轨迹$\tau$的概率就很小；如果有一个回合一$\theta$直没死，因为这种情况很可能发生，所以该回合对应的轨迹$\tau$的概率就很大。我们可以根据$\theta$算出某一个轨迹$\tau$出现的概率，接下来计算$\tau$的总奖励。总奖励使用$\tau$出现的概率进行加权，对所有的$\tau$进行求和，就是期望值。给定一个参数，我们可以计算期望值为

这就引入正文主题了，想让奖励越大越好，就需要梯度，而且是上升来最大化期望奖励，即

不过，由于期望无法直接求导，会用一大堆公式进行推导，得到可以通过采样计算的梯度。数学技巧使用的是$\nabla f(x)=f(x)\nabla logf(x)$.推导公式不放了，感兴趣自己去搜，网上都有，最终公式是这样的，这是梯度的近似计算方法

也很复杂，不看，给出最简单的形式，用于更新$\theta$

其中，$\eta$是学习率，可用Adam等深度学习里的方法来进行调整

注意，一般**策略梯度（policy gradient，PG）**采样的数据只会用一次。我们采样这些数据，然后用这些数据更新参数，再丢掉这些数据。接着重新采样数据，才能去更新参数。

2. 策略梯度实现技巧​

2.1 添加基线（baseline）​

在很多环境中，奖励$R(\tau)$永远是正数（例如迷宫中只要活着就给分）。根据基础公式，只要我们采样到了某个动作，它的概率就会增加。如果某些好的动作没被采样到，它们的相对概率反而会下降，这显然不合理。

解决方法：给奖励减去一个基线 b（通常是所有奖励的平均值）

只有比“平均水平”更好的动作，奖励才会是正的（增加概率）；比平均水平差的动作，奖励会变成负的（降低概率）。

2.2 指派合适的分数 (Assign Suitable Credit)​

在基础算法中，每一局游戏（轨迹$\tau$）得到的总奖励$R(\tau)$会被乘到该局的每一个动作上。但这不公平——也许你开局走得非常好，但最后一步失误导致输了。在基础公式里，开局的那个“好动作”也会被惩罚。

解决方法：不再使用整场游戏的总分，而是使用该动作之后产生的累积奖励,即用$G_t$代替$R(\tau)$

目的是一个动作的评价，只取决于它做完之后发生的奖励。这大大减少了评价中的“噪音”，让梯度更新更准确。

2.3 总结​

看一下了解一下就行，2.2是一个经典的评论员（critic）。后续会专门再写一个评价员算法

3. REINFORCE：蒙特卡洛策略梯度（Monte Carlo Policy Gradient）​

REINFORCE 用的是回合更新的方式，它在代码上的处理上是先获取每个步骤的奖励，然后计算每个步骤的未来总奖励$G_t$，将每个$G_t$代入

$G_t$需要从后往前算，逐步推导到$G_1$，具体表现为

即上一个步骤和下一个步骤的未来总奖励的关系，其实就是原本是(s,a)现在变成了(s,a,G),即

这是一篇使用 PINN 用于通用生物反应器建模的论文。

我们先来看看这篇论文的摘要：

摘要​

英文原文：

Many previous studies have explored hybrid semiparametric models merging Artificial Neural Networks (ANNs) with mechanistic models for bioprocess applications. More recently, Physics-Informed Neural Networks (PINNs) have emerged as promising alternatives. Both approaches seek to incorporate prior knowledge in ANN models, thereby decreasing data dependency whilst improving model transparency and generalization capacity. In the case of hybrid semiparametric modelling, the mechanistic equations are hard coded directly into the model structure in interaction with the ANN. In the case of PINNs, the same mechanistic equations must be “learned” by the ANN structure during the training. This study evaluates a dual-ANN PINN structure for generic bioreactor problems that decouples state and reaction kinetics parameterization. Furthermore, the dual-ANN PINN is benchmarked against the general hybrid semiparametric bioreactor model under comparable prior knowledge scenarios across 2 case studies. Our findings show that the dual-ANN PINN can level the prediction accuracy of hybrid semiparametric models for simple problems. However, its performance degrades significantly when applied to extended temporal extrapolation or to complex problems involving high-dimensional process states subject to time-varying control inputs. The latter is primarily due to the more complex multi-objective training of the dual-ANN PINN structure and to physics-based extrapolation errors beyond the training domain.

翻译：

许多先前的研究探索了将人工神经网络（ANN）与机制模型融合的混合半参数模型，用于生物过程应用。近年来，物理信息神经网络（PINN）作为有前景的替代方案应运而生。这两种方法都试图将先验知识融入 ANN 模型，从而降低对数据的依赖性，同时提高模型的透明度和泛化能力。在混合半参数建模中，机理方程被直接硬编码到模型结构中并与 ANN 交互作用；而在 PINN 中，相同机理方程需由 ANN 结构在训练过程中“学习”获得。本研究针对通用生物反应器问题评估了一种双 ANN-PINN 结构，该结构实现了状态参数与反应动力学参数的解耦。此外，通过两个案例研究，在可比先验知识情境下，将双 ANN PINN 模型与通用混合半参数化生物反应器模型进行基准对比。研究发现：对于简单问题，双 ANN-PINN 可达到与混合半参数模型相当的预测精度；但在扩展时间外推或涉及高维过程状态与时变控制输入的复杂问题中，其性能显著下降。后者主要源于双 ANN-PINN 结构更复杂的多目标训练过程，以及训练域外基于物理的外推误差。

通过摘要可以看出，文章利用 PINN 来求解一类同样由微分方程描述的生物反应器系统。这确实展示了 PINN 在传统物理模型之外的又一类应用场景——它同样能够有效处理其他类型的微分方程。至于该方法的具体实现方式，感兴趣的读者可以继续阅读下文以进一步了解。

abstract​

需求响应（Demand Response, DR）可在美国电力需求峰值中减少约 20%，而建筑物占总电力需求的约 70%。然而，建筑能耗系统动态复杂且难以建模，传统方法难以协调不同建筑或能源系统。强化学习（RL）因其自适应、无需模型的特性，能基于历史与实时数据实现智能能耗控制。 然而，目前 DR 领域的研究缺乏统一标准，实验难以复现，算法性能也难以比较。为此，作者提出 CityLearn —— 一个基于 OpenAI Gym 的开源强化学习仿真环境，可让研究者方便地实现、共享、复现并比较不同的 DR 控制算法。该框架模块化、可扩展，支持多种储能与发电设备模型。

introduction​

美国建筑能耗占全国电力消耗的约 70%，且城市区域的电力需求不断上升，造成输电压力与电价上涨。需求响应（DR）通过激励机制引导用户调整用电模式，从而削减峰值负荷、提高电网稳定性。 然而，为了让 DR 真正有效，需要智能、分布式的负载协调。如果所有设备同时响应相同信号，可能只是“移峰”而非“削峰”。传统控制方法（如 MPC）虽有效，但需依赖昂贵且精确的物理建模。 强化学习（RL）可以在无模型的条件下，通过与环境交互学习最优策略，从实时和历史数据中自动优化建筑能耗管理。但该领域缺乏统一标准，使得不同研究难以比较。为此，作者提出了 CityLearn —— 一个面向城市级能耗优化的强化学习仿真框架，用于统一测试环境、便于算法比较与复现

Abstract​

随着越来越多的分布式能源成为需求侧基础设施的一部分，量化它们在社区规模上提供的能源灵活性非常重要，特别是要了解地理、气候和居住者行为差异对其有效性的影响，以及确定最佳控制策略以加速其在现实世界中的应用。CityLearn 为简单和先进的分布式能源控制算法提供基准测试环境，包括基于规则的、模型预测的和强化学习控制。本文介绍的 CityLearn v2 扩展了 CityLearn v1，它提供了一个模拟环境，利用美国建筑库存数据集的最终用途负载概况来创建虚拟网格交互社区，用于弹性、多代理分布式能源和具有动态乘员反馈的目标控制。这项工作详细介绍了 v2 环境设计，并提供了利用强化学习来管理电池储能系统充放电周期、车辆到电网控制以及热泵功率调制期间的热舒适性的应用示例

一. introduction​

V1 版本很牛，RL 也很牛，但是出于一些缺陷我们创建了 v2 缺点： 灵活性有限 —— v1 的场景结构和数据接口固定，难以扩展到新的建筑类型、设备或能源载体； 可扩展性受限 —— v1 的配置较为僵化，不支持多层能源系统或跨区域交互； 可复现性不足 —— 不同研究者在构建实验时往往需要修改底层代码，导致实验结果难以公平比较。 V2 改进点： v2 版本在体系结构上进行了彻底重构，支持模块化设计和多层能源系统建模。研究者可以轻松地定义新的建筑类型、能源设备、价格信号、碳排放约束、以及能源共享机制。此外，v2 引入了统一的配置文件系统和标准化的评测接口，使不同实验能够方便地复现与对比。 通过这些改进，CityLearn v2 旨在成为一个面向未来的研究平台，支持： · 单智能体与多智能体强化学习； · 集中式与分布式控制； · 电力与热能的多能源协同； · 公平、透明的算法评测与结果共享。

introduction​

这篇文章旨在理解一大堆杂七杂八的，狗屁倒灶的，ai 方向的专用名词，例 AI，NLP，CV，深度学习，强化学习等等等 我相信初学者肯定会对这些名词感到困惑，就如同第一天我在面试时提出的问题： “我就只会数学建模和西瓜皮上的那些算法，好奇的问一下深度学习是啥？” 这个问题对现在的我来说也相当困惑，当然我相信写完这篇文章会让我的理顺这些东西

preliminary knowledge​

首先，给我整个 AI 的框架

人工智能（Artificial Intelligence, AI）
│
├── 机器学习（Machine Learning, ML）
│   ├── 监督学习（Supervised Learning）
│   ├── 无监督学习（Unsupervised Learning）
│   ├── 强化学习（Reinforcement Learning, RL）
│   └── 其他（半监督、主动学习等）
│
├── 深度学习（Deep Learning, DL）
│   ├── 神经网络（CNN, RNN, Transformer）
│   ├── 自监督学习（Self-supervised）
│   ├── 生成模型（GAN, Diffusion, VAE）
│   └── PINNs / SciML（物理引导模型）
│
└── 应用领域
    ├── NLP（自然语言处理）
    ├── CV（计算机视觉）
    ├── Speech（语音）
    └── 多模态 / 大模型（GPT, Gemini, etc.）

代码路径：https://github.com/zqqqqqqj1110/CityLearn_exp.git​

target

比较不同任务配置下，RBC（Rule-Based Control）与 RLC（Reinforcement Learning Control）在能源、排放、峰值与舒适度方面的表现。 数量： 共 17 个任务（单建筑、多建筑、单目标、多目标） 输出指标：

1. Electricity Cost [$]
2. Emissions [kg CO₂]
3. Peak Demand [kW]
4. Discomfort Penalty [–]

准备环境

创建环境，准备 citylearn 的 conda env

conda create -n citylearn python=3.10 -y
conda activate citylearn

安装 city learn V2

git clone https://github.com/intelligent-environments-lab/CityLearn.git
cd CityLearn
pip install -e .    # 源码控制版，仅用于复现
pip install citylearn   # 后续试验可以直接用这个下载

introduction​

这篇文章旨在理解一大堆杂七杂八的，狗屁倒灶的，ai 方向的专用名词，例 AI，NLP，CV，深度学习，强化学习等等等 我相信初学者肯定会对这些名词感到困惑，就如同第一天我在面试时提出的问题： “我就只会数学建模和西瓜皮上的那些算法，好奇的问一下深度学习是啥？” 这个问题对现在的我来说也相当困惑，当然我相信写完这篇文章会让我的理顺这些东西

preliminary knowledge​

首先，给我整个 AI 的框架

人工智能（Artificial Intelligence, AI）
│
├── 机器学习（Machine Learning, ML）
│   ├── 监督学习（Supervised Learning）
│   ├── 无监督学习（Unsupervised Learning）
│   ├── 强化学习（Reinforcement Learning, RL）
│   └── 其他（半监督、主动学习等）
│
├── 深度学习（Deep Learning, DL）
│   ├── 神经网络（CNN, RNN, Transformer）
│   ├── 自监督学习（Self-supervised）
│   ├── 生成模型（GAN, Diffusion, VAE）
│   └── PINNs / SciML（物理引导模型）
│
└── 应用领域
    ├── NLP（自然语言处理）
    ├── CV（计算机视觉）
    ├── Speech（语音）
    └── 多模态 / 大模型（GPT, Gemini, etc.）

按照参差结构来讲，先从最简单的开始吧

1. 应用领域​

搜索算法，符号推理这些其实都可以类比到实习中的“搜推广”（搜索推荐广告）算法工程师。这些东西其实都可以归结为应用领域或技术范式。如下所示

2. 机器学习​

机器学习就是大部分西瓜皮上的内容了，他的本意就是“让计算机自己去学习”，所以就会自然而言的牵扯到两大类别，即无监督学习和有监督学习，具体含义如下

对于强化学习而言，这部分会在后续着重介绍（因为我真的不懂）。但是一般而言，按照“想让机器学到什么”的定义，又可如下分类 · 监督学习用于“从已有示例中学习” · 无监督学习用于“理解数据结构” · 强化学习用于“学习行动策略”

3. 深度学习​

深度学习是机器学习的一个重要分支，可以理解为使用多层神经网络（Neural Networks）自动学习数据特征的一类方法 换句话说，它依然遵循“最小化误差（loss function）”的思想，但与传统机器学习不同，
深度学习不再需要人手去“提取特征”，而是通过层层网络结构自动完成特征提取与抽象表示

从集合关系上看： 深度学习 ⊂ 神经网络 ⊂ 机器学习 ⊂ 人工智能 例子：

difference between Deep Learning（DL） and machine Learning（ML）​

尽管两者的本质都是最小化误差（如 loss function），但核心目的是不同的。ML 的目的是寻找使预测误差最小的参数。（比如在 n 次线性函数中找最优参数，神经网络调整通过 Adam 反向传播调整网络权重）

DL 也确实是继承了这个想法（最小化误差），但它的关键区别在于 “模型复杂度” 和 “特征获取方式”

其实可以理解为，DL 本质就是神经网络，只是这个网络又大（神经元）又深（多层）。深度学习不只是有神经网络，还包括优化算法、损失函数、正则化、数据增强等。神经网络是模型，深度学习是方法。 最大的目的就是：为了学习特征。区别在于可以更好的处理高度非线形问题

强化学习​

说了这么多，终于可以讲强化学习了，强化学习是让智能体（Agent）通过与环境（Environment）交互，并根据奖励（Reward）反馈，学习最优决策策略（Policy）的方法。 需要注意的是，这是一个最大化优化，不是 loss 这样的最小化优化（奖励必然是越多越好）

继续举例五大基本元素

p-code 如下：

for episode in range(N):
    state = env.reset()     # Agent观察环境（init啦其实就是）
    while not done:     # 开始训练
        action = agent.select_action(state)     # 选择一个动作
        next_state, reward, done = env.step(action)     # 环境给出新的状态和奖励；
        agent.learn(state, action, reward, next_state)  # Agent根据奖励更新策略
        state = next_state

所以，强化学习不是预测一个矢量或标量，他的目的应该是学习一种策略

ps：some cases

这是一篇使用 VPinn 来求解 Navier-Stokes 方程的论文。

我们先来看看这篇论文的摘要：

摘要​

英文原文：

Physics-informed neural networks (PINNs) are able to solve partial differential equations (PDEs) by incorporating the residuals of the PDEs into their loss functions. Variational Physics-Informed Neural Networks (VPINNs) and hpVPINNs use the variational form of the PDE residuals in their loss function. Although hp-VPINNs have shown promise over traditional PINNs, they suffer from higher training times and lack a framework capable of handling complex geometries, which limits their application to more complex PDEs. As such, hp-VPINNs have not been applied in solving the Navier-Stokes equations, amongst other problems in CFD, thus far. FastVPINNs was introduced to address these challenges by incorporating tensor-based loss computations, significantly improving the training efficiency. Moreover, by using the bilinear transformation, the FastVPINNs framework was able to solve PDEs on complex geometries. In the present work, we extend the FastVPINNs framework to vector-valued problems, with a particular focus on solving the incompressible Navier-Stokes equations for two-dimensional forward and inverse problems, including problems such as the lid-driven cavity flow, the Kovasznay flow, and flow past a backward-facing step for Reynolds numbers up to 200. Our results demonstrate a 2x improvement in training time while maintaining the same order of accuracy compared to PINNs algorithms documented in the literature. We further showcase the framework’s efficiency in solving inverse problems for the incompressible Navier-Stokes equations by accurately identifying the Reynolds number of the underlying flow. Additionally, the framework’s ability to handle complex geometries highlights its potential for broader applications in computational fluid dynamics. This implementation opens new avenues for research on hp-VPINNs, potentially extending their applicability to more complex problems.

翻译：

物理信息的神经网络（PINN）能够通过将 PDE 的残差纳入其损失函数来解决部分微分方程（PDE）。变异物理信息的神经网络（VPINN）和 HPVPINNS 在其损失函数中使用 PDE 残差的变异形式。尽管 HP-vpinns 对传统的 PINN 表现出了希望，但它们遭受了较高的训练时间，并且缺乏能够处理复杂几何形状的框架，从而将其应用限制在更复杂的 PDES 中。因此，迄今为止，尚未应用 HP-VPINN 在求解 Navier-Stokes 方程中，以及 CFD 中的其他问题。引入了 FASTVPINNS，通过结合基于张量的损失计算，从而显着提高训练效率，以应对这些挑战。此外，通过使用双线性转换，FastVpinns 框架能够在复杂的几何形状上求解 PDE。在目前的工作中，我们将 FASTVPINNS 框架扩展到了矢量值问题，特别着眼于解决不可压缩的 Navier-Stokes 方程，以解决二维向前和反向问题，包括诸如盖子驱动的腔流，kovasznay 流量以及以后的阶段进行阶段的阶段，以改进阶段的时间，并将其进行了训练。与文献中记录的 PINNS 算法相比，准确性。我们通过准确识别基础流的雷诺数数量，进一步展示了该框架在解决不可压缩的 Navier-Stokes 方程中的反问题方程的效率。此外，该框架处理复杂几何形状的能力突出了其在计算流体动力学中更广泛应用的潜力。该实施为 HP-VPINNS 研究开辟了新的途径，有可能将其适用性扩展到更复杂的问题上。

这是一篇比较巧妙地方法（MLGCC）解决多区域微分方程的论文。

这篇论文先从介绍入手，来整体的看看这篇论文：

在本文中，我们将以下抛物线方程与两个非均匀跳跃条件视为

其中，$I_1 = (−1,0), I_2 = (0,1)$ 和 $I = (−1,1),\epsilon |_{I_i} = \epsilon_i$ 是正分段常数，跳跃由 $[v]_0 = v(0+)−v(0−)$ 定义，$α,β$ 是常数。这种跳跃条件在许多地区都会出现[14,2,12]。开发了多域 LegendreGalerkin Chebyshev-collocation（MLGCC）方法来解决该问题（1.1）。该方案基于勒让德方法，但右项和初始项由切比雪夫-高斯-洛巴托 （CGL） 点并置。时间离散化采用 CrankNicolson 方法。该方案基本上处理了第一个跳跃条件，而自然处理了第二个跳跃条件。如[15]所示，构造了适当的基函数来处理并行求解问题（1.1）的接口。推导了稳定性和最佳收敛速率。考虑了 MLGCC 方法在一维（1D）Maxwell 方程和 1D 两相 Stefan 问题中的应用。

文章整理如下。在第 2 节中，可以介绍一些符号和方案。在第 3 节中，给出了近似结果。在第 4 节中，我们证明了全离散方案的稳定性和收敛性。给出了一些相应的数值结果。在第 5 节和第 6 节中，我们使用我们的方法求解了一维麦克斯韦方程组和一维两相 Stefan 问题，并给出了数值结果。

这是一篇使用同调法与 PINN 相结合解决非线性椭圆微分方程的论文，并处理了不规则边界区域。

摘要​

摘要原文：

Physics-informed neural networks (PINNs) based machine learning is an emerging framework for solving nonlinear differential equations. However, due to the implicit regularity of neural network structure, PINNs can only find the flattest solution in most cases by minimizing the loss functions. In this paper, we combine PINNs with the homotopy continuation method, a classical numerical method to compute isolated roots of polynomial systems, and propose a new deep learning framework, named homotopy physics-informed neural networks (HomPINNs), for solving multiple solutions of nonlinear elliptic differential equations. The implementation of an HomPINN is a homotopy process that is composed of the training of a fully connected neural network, named the starting neural network, and training processes of several PINNs with different tracking parameters. The starting neural network is to approximate a starting function constructed by the trivial solutions, while other PINNs are to minimize the loss functions defined by boundary condition and homotopy functions, varying with different tracking parameters. These training processes are regraded as different steps of a homotopy process, and a PINN is initialized by the well-trained neural network of the previous step, while the first starting neural network is initialized using the default initialization method. Several numerical examples are presented to show the efficiency of our proposed HomPINNs, including reaction-diffusion equations with a heart-shaped domain.

摘要翻译：

基于物理信息神经网络（PINNs）的机器学习是一种新兴的非线性微分方程求解框架。然而，由于神经网络结构的隐含规律性，PINNs 在大多数情况下只能通过最小化损失函数找到最平坦的解。在本文中，我们将 PINNs 与同调延续法（一种计算多项式系统孤立根的经典数值方法）相结合，提出了一种新的深度学习框架，命名为同调物理信息神经网络（HomPINNs），用于求解非线性椭圆微分方程的多解。HomPINN 的实现是一个同调过程，由一个名为起始神经网络的全连接神经网络的训练和多个具有不同跟踪参数的 PINN 的训练过程组成。起始神经网络用于逼近由三元解构建的起始函数，而其他 PINN 则用于最小化由边界条件和同调函数定义的损失函数，这些函数随不同的跟踪参数而变化。这些训练过程被重新划分为同调过程的不同步骤，一个 PINN 由上一步训练有素的神经网络初始化，而第一个起始神经网络则使用默认初始化方法初始化。本文列举了几个数值示例来说明我们提出的 HomPINN 的效率，其中包括具有心形域的反应扩散方程。

这是一篇变系数的波动方程，提出了一种新的格式。

摘要​

摘要原文：

A new and efficient neural-network and finite-difference hybrid method is developed for solving Poisson equation in a regular domain with jump discontinuities on embedded irregular interfaces. Since the solution has low regularity across the interface, when applying finite difference discretization to this problem, an additional treatment accounting for the jump discontinuities must be employed. Here, we aim to elevate such an extra effort to ease our implementation by machine learning methodology. The key idea is to decompose the solution into singular and regular parts. The neural network learning machinery incorporating the given jump conditions finds the singular solution, while the standard five-point Laplacian discretization is used to obtain the regular solution with associated boundary conditions. Regardless of the interface geometry, these two tasks only require supervised learning for function approximation and a fast direct solver for Poisson equation, making the hybrid method easy to implement and efficient. The two- and three-dimensional numerical results show that the present hybrid method preserves second-order accuracy for the solution and its derivatives, and it is comparable with the traditional immersed interface method in the literature. As an application, we solve the Stokes equations with singular forces to demonstrate the robustness of the present method.

摘要翻译：

一种新型高效的神经网络与有限差分混合方法被开发用于求解具有嵌入式不规则界面跳变不连续性的规则域中的泊松方程。由于解在界面处具有较低的正则性，当对该问题应用有限差分离散化时，必须采用额外处理以考虑跳变不连续性。本文旨在通过机器学习方法将此额外处理简化，以提升实现效率。

核心思想是将解分解为奇异部分和规则部分。神经网络学习机制结合给定的跳变条件求解奇异解，而标准五点拉普拉斯离散化用于获得满足边界条件的规则解。无论界面几何如何，这两个任务仅需监督学习进行函数逼近和快速直接求解器求解泊松方程，使混合方法易于实现且高效。二维和三维数值结果表明，本混合方法可保持解及其导数的二阶精度，且与文献中传统的浸入式界面方法相当。作为应用示例，我们通过求解带有奇异力的斯托克斯方程，验证了本方法的鲁棒性。

这是一篇变系数的波动方程，提出了一种新的格式。

摘要​

摘要原文：

This article presents a new analytical formula for the Cauchy problem of the wave equation with variable coefficients, which is a much simpler solution than that given by the Poisson formula. The derivation is based on the variation-of-constants formula and the theory of pseudodifferential operator. The formula is applied to an example to illustrate the feasibility.

摘要翻译：

本文提出了一个新的解析公式，用于求解具有变系数的波方程的柯西问题，该公式比泊松公式给出的解要简单得多。该公式的推导基于常数变换公式和伪微分算子理论。该公式被应用于一个例子，以说明其可行性。

这是一篇关于处理变系数边界问题的 PINN 论文。

摘要​

摘要原文：

This paper proposes a novel and general framework of the discontinuity-removing physicsinformed neural networks (DR-PINNs) for addressing elliptic interface problems. In the DR-PINNs, the solution is split into a smooth component and a non-smooth component, each represented by a separate network surrogate that can be trained either independently or together. The decoupling strategy involves training the two components sequentially. The first network handles the non-smooth part and pre-learns partial or full jumps to assist the second network in learning the complementary PDE conditions. Three decoupling strategies of handling interface problems are built by removing some jumps and incorporating cusp-capturing techniques. On the other hand, the decoupled approaches rely heavily on the cusp-enforced level-set function and are less efficient due to the need for two separate training stages. To overcome these limitations, a novel DR-PINN coupled approach is proposed in this work, where both components learn complementary conditions simultaneously in an integrated single network, eliminating the need for cusp-enforced level-set functions. Furthermore, the stability and accuracy of training are enhanced by an innovative architecture of the lightweight feedforward neural network (FNN) and a powerful geodesic acceleration Levenberg-Marquardt (gd-LM) optimizer. Several numerical experiments illustrate the effectiveness and great potential of the proposed method, with accuracy outperforming most deep neural network approaches and achieving the state-of-the-art results.

摘要翻译：

本文提出了一种新型且通用的断续性消除物理信息神经网络（DR-PINNs）框架，用于解决椭圆型界面问题。在 DR-PINNs 中，解被分解为光滑部分和非光滑部分，每个部分由独立的神经网络代理表示，这些代理可以单独训练或共同训练。解耦策略涉及依次训练这两个部分。第一个网络处理非光滑部分，并预先学习部分或全部跳跃，以协助第二个网络学习互补的偏微分方程（PDE）条件。通过去除部分跳跃并结合尖点捕获技术，构建了三种处理界面问题的解耦策略。另一方面，解耦方法高度依赖于尖点强制水平集函数，且由于需要两个独立的训练阶段而效率较低。为克服这些局限性，本文提出了一种新型 DR-PINN 耦合方法，其中两个组件在集成单一网络中同时学习互补条件，消除了对尖点强制水平集函数的需求。此外，通过轻量级前馈神经网络（FNN）的创新架构和强大的几何加速 Levenberg-Marquardt（gd-LM）优化器，训练的稳定性和准确性得到提升。多个数值实验验证了所提方法的有效性和巨大潜力，其精度显著优于现有方法。

这是一篇开山之作提出了一个深度学习框架 DeepONet 用于求解偏微分方程的求解器，这篇论文介绍了原理。

摘要​

摘要原文：

While it is widely known that neural networks are universal approximators of continuous functions, a less known and perhaps more powerful result is that a neural network with a single hidden layer can approximate accurately any nonlinear continuous operator [5]. This universal approximation theorem is suggestive of the potential application of neural networks in learning nonlinear operators from data. However, the theorem guarantees only a small approximation error for a sufficient large network, and does not consider the important optimization and generalization errors. To realize this theorem in practice, we propose deep operator networks (DeepONets) to learn operators accurately and efficiently from a relatively small dataset. A DeepONet consists of two sub-networks, one for encoding the input function at a fixed number of sensors $x_i = 1, ... , m$ (branch net), and another for encoding the locations for the output functions (trunk net). We perform systematic simulations for identifying two types of operators, i.e., dynamic systems and partial differential equations, and demonstrate that DeepONet significantly reduces the generalization error compared to the fully-connected networks. We also derive theoretically the dependence of the approximation error in terms of the number of sensors (where the input function is defined) as well as the input function type, and we verify the theorem with computational results. More importantly, we observe high-order error convergence in our computational tests, namely polynomial rates (from half order to fourth order) and even exponential convergence with respect to the training dataset size.

摘要翻译：

尽管神经网络是连续函数的通用逼近器这一事实广为人知，但一个较少为人所知且可能更强大的结果是：具有单个隐藏层的神经网络能够精确逼近任何非线性连续算子。这一通用逼近定理暗示了神经网络在从数据中学习非线性算子方面的潜在应用。然而，该定理仅保证在网络规模足够大时存在较小的逼近误差，并未考虑重要的优化误差和泛化误差。为了在实践中实现这一定理，我们提出**深度算子网络（DeepONets）**以从相对较小的数据集准确高效地学习算子。一个 DeepONet 由两个子网络组成：一个用于在固定数量的传感器上编码输入函数 $x_i = 1, ..., m$（分支网络），另一个用于编码输出函数的位置（主干网络）。我们通过系统性模拟识别两种类型的算子，即动态系统和偏微分方程，并证明 DeepONet 相较于全连接网络显著降低了泛化误差。我们还从理论上推导了近似误差与传感器数量（即输入函数定义的传感器数量）以及输入函数类型之间的依赖关系，并通过计算结果验证了该定理。更重要的是，我们在计算测试中观察到高阶误差收敛，即多项式收敛率（从半阶到四阶）甚至与训练数据集大小相关的指数收敛。

这是一篇使用谱元方法与 PINN（物理信息神经网络）相结合的论文。

摘要​

摘要原文：

Spectral methods are an important part of scientific computing’s arsenal for solving partial differential equations (PDEs). However, their applicability and effectiveness depend crucially on the choice of basis functions used to expand the solution of a PDE. The last decade has seen the emergence of deep learning as a strong contender in providing efficient representations of complex functions. In the current work, we present an approach for combining deep neural networks with spectral methods to solve PDEs. In particular, we use a deep learning technique known as the Deep Operator Network (DeepONet) to identify candidate functions on which to expand the solution of PDEs. We have devised an approach that uses the candidate functions provided by the DeepONet as a starting point to construct a set of functions that have the following properties: (1) they constitute a basis, (2) they are orthonormal, and (3) they are hierarchical, i.e., akin to Fourier series or orthogonal polynomials. We have exploited the favorable properties of our custom-made basis functions to both study their approximation capability and use them to expand the solution of linear and nonlinear time-dependent PDEs. The proposed approach advances the state of the art and versatility of spectral methods and, more generally, promotes the synergy between traditional scientific computing and machine learning.

摘要翻译：

谱方法是科学计算用于求解偏微分方程 (PDE) 的重要工具。然而，它们的适用性和有效性在很大程度上取决于用于扩展偏微分方程解的基函数的选择。近十年来，深度学习异军突起，成为提供复杂函数高效表示的有力竞争者。在当前的工作中，我们提出了一种将深度神经网络与光谱方法相结合来求解 PDE 的方法。特别是，我们使用一种被称为深度算子网络（DeepONet）的深度学习技术来识别候选函数，并在此基础上扩展 PDE 的求解。我们设计了一种方法，以 DeepONet 提供的候选函数为起点，构建一组具有以下特性的函数：(1) 它们构成一个基础；(2) 它们是正交的；(3) 它们是分层的，即类似于傅里叶级数或正交多项式。我们利用定制基函数的有利特性，研究了它们的近似能力，并利用它们扩展了线性和非线性时变 PDE 的解。所提出的方法推进了频谱方法的技术水平和多功能性，更广泛地说，促进了传统科学计算与机器学习之间的协同作用。

其实只要细读了他的摘要就可以发现这篇论文的做法比较独特，他并不是把机器学习与谱方法相融合，而是采取了一种分阶段的模式，第一步是使用 DeepONet 去识别候选函数，再利用常规的谱方法来完成剩下的计算工作，他并不是一整块的模型而是耦合度低的分阶段模型。这种思想其实结合误差达到 $10^{-4}$ 到 $10^{-8}$ 就能够理解，不过也算是给机器学习融合谱方法提供了一种思路，接下来我们详细的阅读这篇文章的结果以及方法。

本文将从三部分，即 GAN 模型的理论部分，代码（实践）部分及 SRGAN 的消融试验部分展开介绍

1. GAN（Generative Adversarial Network）生成对抗网络​

核心：由两个神经网络——生成器（Generator）和判别器（Discriminator）组成，通过博弈过程相互提升。 · 生成器：试图“伪造”以假乱真的数据。 · 判别器：判断输入是真实数据还是生成器伪造的。 · 训练目标：生成器希望骗过判别器，判别器希望准确识别真假。 本质上是一个最大最小问题：

2. cGAN（Conditional GAN）条件生成对抗网络​

核心：在 GAN 的基础上，引入“条件”信息（如标签、图像、文本等） · 生成器和判别器都接收条件变量 · G（z，y）：在条件 y 下生成图像 · D（x，y）：判断图像是否为在条件 y 下真实的 用途：图像翻译（如黑白图像上色）、语义图生成图像、文本生成图像 目标函数：

1. 摘要​

约 15% 的全球人口受到各种残障或视力障碍的影响，但许多移动端的用户体验（UX）设计师和开发者在开发 App 时并未重视可访问性问题。这意味着每七个人中就有一个用户在使用 App 时面临不平等的体验，这不仅影响用户，也可能违反相关法规。实际上，如果 App 开发时考虑可访问性，不仅能提升整体用户体验，还能提升商业价值。因此，已有不少研究和检测工具被提出用于识别可访问性问题。

然而，与检测相比，修复工作明显滞后，尤其是“颜色相关的可访问性问题”——比如文字对比度不足和图片对比度不佳，这类问题极大地影响了低视力用户和老年用户的使用体验，而当前的修复方法对此无能为力。

为此，我们提出了 Iris：一种自动化且具备上下文感知能力的方法，用于修复颜色相关的可访问性问题。该方法通过设计一致性的颜色替换策略和属性定位算法，在修复问题的同时保持 UI 风格的一致性。实验显示，Iris 可达到 91.38% 的修复成功率，且效率较高。用户调研也表明其结果令人满意，开发者反馈积极。我们在 GitHub 上提交的 40 个 Pull Request 中已有 9 个被合并，另有 4 个正在积极沟通后续修复。Iris 工具现已开源，旨在推动移动可访问性修复领域的进一步研究。

如果你读到这里，或许你已经准备好去探索这个领域的规律与本质。在我们看来，**认真对待每一篇论文，是科研之路的起点，更是最重要的一步。**正如教育部“长江学者”特聘教授尹芝南所言：

“阅读我们的文献，是从事科学研究的基础，也是我们研究生的必修课程。”

从头到尾逐字翻译或阅读一篇科技论文，实际上是效率最低的方式。经验丰富的科研人员通常会优先关注文章中最关键的信息，以进行快速判断其研究价值与相关性。

正确有效的阅读一篇科技论文​

阅读一篇科技论文效率最低的方法就是从头到尾翻译。专家研究人员会从文章中较为关键的点进行查找发现。一般来说，大多数科技论文会分为五个部分，如图红色部分：

• Abstract
• Introduction
• Method
• Result
• Discussion

相信看到这里的朋友，已经对一篇科研论文（Research Article）的基本结构相当熟悉了。科研工作者最常撰写的文章类型之一就是采用 IMRaD 模式 的研究论文，即包括以下几个部分：

• I – Introduction（引言）
• M – Methods（方法）
• R – Results（结果）
• A – Abstract（摘要）
• D – Discussion（讨论）

我将结合自己的经历，分享论文写作的一般流程。需要注意的是，论文的撰写顺序通常并不等同于其最终的排版结构。在科研实践中，写作往往是从已有的研究结果出发，逐步向前、向后延展的。

通常，在完成一段时间的实验或建模工作后，我们首先获得的是一组数据或研究结果。因此，写作往往是从 Results（结果） 开始，根据结果再去梳理并书写 Methods（方法），说明这些结果是如何得到的。随后撰写 Discussion（讨论），对结果进行分析和解释，进一步明确其意义与不足之处。

在此基础上，我们再回到前面，撰写 Introduction（引言），梳理研究背景、动机、已有工作与创新点。最后撰写 Abstract（摘要），对全文进行简洁总结。

1. 安装 linux​

这就不多说了，自己搞一个虚拟机，我用的是 Centos7。

ps：如果使用的是学校集群的话，注意在修改密码中改一下自己的密码，开启后账号为：root，密码自定义（注意是暗文，你敲进去是不会显示的）结束了 enter 即可

2. 预先安装​

首先要安装 anaconda，为了不污染环境

-- 安装linux安装包（如果报错自己去anaconda网站找地址）
wget https://repo.anaconda.com/archive/Anaconda3-2023.07-Linux-x86_64.sh

-- 解压anaconda，后面的就是刚刚安装好的名字
bash Anaconda3-2023.07-Linux-x86_64.sh

-- 更新环境变量
source ~/.bashrc

1. 测出数据部分​

在通过前文的处理之后，我们得到了两个输出文件，分别为 raw_feature_bc_matrix 和 filter_feature_bc_matrix。前者为原始数据，后者为 cellranger 经过自己处理后的数据，后续的分析会基于 filter_feature_bc_matrix 文件夹（上游比对分析产生的三个文件）。文件夹目录如下

--filter_feature_bc_matrix
----barcodes.tsv
----features.tsv
----matrix.mtx

逐一解释：

**barcodes.tsv：**细胞标签

**features.tsv：**基因 ID

**matrix.mtx：**表达数据

后续我们会使用 seurat（R 语言）进行分析

在单细胞 RNA 测序分析中，聚类之后筛选差异基因的主要目的是为了深入理解不同细胞群体之间的生物学差异。首先先看我们筛选出来的数据并对其进行解释

**p_val：**基因表达量差异 P 值（一般不看这个）

**p_val_adj：**校正后的 P 值（一般看这个）

**avg_log2FC：**基因在该细胞簇中与其他细胞簇表达量差异倍数的 log 值，一般大于 2 是最好的效果，说明差异很大

**pct.1：**在该细胞簇中表达该基因的细胞数量占比

**pct.2：**在其他细胞簇中表达该基因的细胞数量占比平均值

**cluster：**在哪一类簇中

**gene：**名字

**myroc：**roc 评分，范围从[0,1] ，越大越好

通过前文我们可以提取出差异基因，然而差异基因的数量较多，对其进行分析会十分冗长，因此我们可以采取富集分析的方式进行归类。富集的意思是表示差异基因或者差异物质中注释到某个代谢通路的基因或者物质数目在所有差异基因或者物质中的比例显著大于背景基因或物质中注释到某个代谢通路的基因或物质数目在所有背景基因或者物质中的比例。简而言之一句话概括：该差异基因在特定的通路上占比很大

5.1 GO 富集分析​

主要用来看基因的三个方面，分别是分子功能、细胞组分、参与的生物过程。

举例，铁离子结合的 GO term 是 GO:0005506，如果我们对所得到的差异基因进行 GO 富集分析后得到该 term 富集，则我们可以认为我们所研究的现象可能与铁离子结合有关系

进行 go 分析时，可以得到如下数据：

参数解释：

category： Gene Ontology 数据库中唯一的标号信息

**over_represented_pvalue：**富集分析 P 值，P 值越小越显著

under_represented_pvalue：

**numDEInCat：**该功能类下的差异基因数目

**numInCat：**该功能类下的基因数目

**term：**Gene Ontology 功能的描述信息

**ontology：**该 GO 的类别(CC，细胞组分；BP，生物进程；MF，分子功能)。

接着，还可以可视化 DAG 图，分支代表包含关系，从上至下所定义的功能范围越来越小，一般选取 GO 富集分析的结果前 5 位作为有向无环图的主节点，颜色的深浅代表富集程度。概括的说， 可以分析 GO terms 在富集分析中是否显著，并且 terms 是如何相互关联的

这两块代码含量都比较少，大部分通过在线分析就可以出结果

构建差异表达基因编码的蛋白质之间的相互作用网络，识别关键调控蛋白质或蛋白质复合物。

输出的是 PPI 网络图及其分析结果，发现核心蛋白质。

在线分析网站：356 items (Macaca mulatta) - STRING interaction network (string-db.org)

可选选项：

1. 隐藏无关联节点
2. 节点多少可由 score 设置
3. 保存为 tsv 文件（as tabular test output），进入到 cytoscape 进行美化
4. 多个选 Multiple proteins；单个选 Protein by name

在进行了聚类之后，其实各细胞是否具有同种生存状态是未知的。拟时序分析的目的就在于将细胞分为不同的分支，将各点（细胞）体现在不同的时间坐标中，从而了解各细胞的状态定位

在做拟时序分析的时候，采取的是机器学习方法（无监督和有监督），因此需要一定的生物学知识对图标进行判断，图中主要是为了表达细胞之间（簇）表达谱系的连续性，因此方向未必与现实情况相同（需要在代码中加入 reserve）

举个例子：B 细胞不会分化为 NK 细胞，但在图中就会如此，这就是 reserve 的作用

本文主要采取无监督的方法进行分析

tips：无监督就是没有真实数据，有监督就是包含一定的真实数据

• 无监督数据：常见的如单细胞 RNA 测序数据，在特定的发育阶段采集了样本，但不确定细胞的确切时间顺序。
• 有监督数据：例如药物处理实验，在不同时间点采集了单细胞样本，记录了每个样本的处理时间，通过这些时间点信息可以进行有监督的拟时序分析。

首先，使用 monocol2 创建 CellDataset 对象后，就有了拟时分析结果的可视化，我们可以将其分为：

state 状态：

代表了细胞在某一生物学过程中所处的不同阶段。例如，在细胞分化过程中，初始的未分化状态、不同分化路径中的中间状态，以及终末分化状态，都会被标记为不同的“state”。

这是一篇关于使用数据驱动方法实现的 Physics-Informed Deep Learning（PINN）经典论文。

论文的来源​

    首先，本人通过搜索很多 PINN 的论文，发现许多论文都在引用这篇论文，在好奇心的驱使下就在 google 学术上搜索了这篇论文，我们可以看到出现了两个版本，从标题名上看大致相同，作者也没变化。据开组会时，覃老师介绍说可能是因为前面这个版本是相当于没有正式发表还处于一个草稿阶段，后面那篇是经过整理并发表到了比较好的期刊中，我们可以从引用量(比较粗的红线)以及 easyScholar (比较细的红线)打上的标签还有作者希望我们引用这项工作的论文排名(作者更希望我们引用 2019 年正式分布的那篇)中看到区别，但不妨碍这几篇论文的优秀性，总的来说 M Raissi 等人的工作是非常出色的。