Physics Informed Deep Learning (Part I) Data-driven Solutions of Nonlinear Partial Differential Equations

这是一篇关于使用数据驱动方法实现的 Physics-Informed Deep Learning（PINN）经典论文。

论文的来源

    首先，本人通过搜索很多 PINN 的论文，发现许多论文都在引用这篇论文，在好奇心的驱使下就在 google 学术上搜索了这篇论文，我们可以看到出现了两个版本，从标题名上看大致相同，作者也没变化。据开组会时，覃老师介绍说可能是因为前面这个版本是相当于没有正式发表还处于一个草稿阶段，后面那篇是经过整理并发表到了比较好的期刊中，我们可以从引用量(比较粗的红线)以及 easyScholar (比较细的红线)打上的标签还有作者希望我们引用这项工作的论文排名(作者更希望我们引用 2019 年正式分布的那篇)中看到区别，但不妨碍这几篇论文的优秀性，总的来说 M Raissi 等人的工作是非常出色的。

    他们也将这篇论文的工作产生的代码无私的奉献了出来，可以通过访问 Github 来查看相关代码，上面的代码是 tensorflow 的 1 版本写的，到现在 tensorflow 已经不支持 1 版本的 python 包安装，所以可能需要将上面的代码写成 2 版本的形式才能运行。 👉点我查看 Github 仓库

    这篇论文被视为数据驱动的 PINN 的研究工作的思想源头，有打算实现数据驱动的 PINN 工作的人可以先稍微熟悉该论文。他的论文分为三个部分，现在来介绍第一部分。原论文(Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations)

    想要明白 PINN，先从 PINN 是什么说起，PINN 其实是 Physics Informed Deep Learning 的缩写，中文中比较准确的翻译是物理信息深度学习，人话就是结合了物理信息的深度学习模型。

    其实将机器学习用在求解偏微分方程上不是什么难事，但是直接用肯定是不行的，主要面对了几个问题，只要能很好的解决以下问题，那问题就迎刃而解了。

数据采集：数据采集的成本太高几乎无法实现，尤其是对小样本的数据样本，绝大多数的机器学习技术缺乏鲁棒性，无法提供任何收敛保证。

我们也来探讨一下传统方法的优劣，传统方法会有（维度灾难），传统数值算法或者主流软件都需要构造剖分，如果维度太高会造成维度灾难，对于 d 维空间，假设每个维度打 $n$ 个网格点，那么一共需要 $d^n$ 个网格点。

由此的话，我们开始想到用神经网络来解决数值算法问题。

市面上主要神经网络求解偏微分方程模型：

方法	二阶导	惩罚系数	高维空间	测试函数	精度	时间
Deep Ritz	×	√	√	×	good	long
Deep Galerkin	×	×	×	√	better	long
PINN	√	×	×	×	best	longest
PFNN	×	×	√	×	better	longest

Abstract（摘要）

    We introduce physics informed neural networks– neural networks that are trained to solve supervised learning tasks while respecting any given law of physics described by general nonlinear partial differential equations. In this two part treatise, we present our developments in the context of solving two main classes of problems: data-driven solution and data-driven discovery of partial differential equations. Depending on the nature and arrangement of the available data, we devise two distinct classes of algorithms, namely continuous time and discrete time models. The resulting neural networks form a new class of data-efficient universal function approximators that naturally encode any underlying physical laws as prior information. In this first part, we demonstrate how these networks can be used to infer solutions to partial differential equations, and obtain physics-informed surrogate models that are fully differentiable with respect to all input coordinates and free parameters.

    摘要的内容如上，建议多读几次，本笔记比较粗浅，有时间建议看看原文。

    翻译成中文（deepl 翻译）：我们介绍了物理学上的神经网络 - 神经网络被训练来解决监督学习任务，同时尊重由一般非线性偏微分方程描述的任何特定的物理学规律。在这两部分论文中，我们介绍了我们在解决两类主要问题方面的发展：数据驱动的解决方案和数据驱动的偏微分方程的发现。根据可用数据的性质和安排，我们设计了两类不同的算法，即连续时间和离散时间模型。由此产生的神经网络形成了一类新的数据高效的通用函数近似器，自然地将任何潜在的物理规律编码为先验信息。在这第一部分，我们展示了这些网络如何被用来推断偏微分方程的解决方案，并获得物理信息的代用模型，这些模型对于所有输入坐标和自由参数是完全可微的。

原文中有一段话：These developments are presented in the context of two main problem classes: data-driven solution and data-driven discovery of partial differential equations.这些进展围绕两类核心问题展开：数据驱动的 PDE 求解与 PDE 结构的自动发现，分别引导了 PINN 在数据利用和物理约束建模两个方向上的持续优化。

连续时间模型

作者提出了一个一般形式的参数化和非线性偏微分方程：

$$u_t+\mathcal{N}[u;\lambda]=0,$$

其中 $u(t; x)$ 表示潜在（隐藏）解和 $\mathcal{N} [·; λ]$ 是参数为 $\lambda$ 的非线性算子。

Burgers 方程

$$u_{t}+uu_{x}-(0.01/\pi)u_{xx}=0,\quad x\in[-1,1],\quad t\in[0,1], \\ u(0,x)=-\sin(\pi x), \\ u(t,-1)=u(t,1)=0.$$

与此同时，作者将 $f(x,t)$ 定义为

$$f:=u_{t}+u u_{x}-(0.01 / \pi) u_{x x}$$

并使用 Python 简单的将 $u(x,t)$ 定义为：

def u(t, x):
    u = neural_net(tf.concat([t,x],1), weights, biases)
    return u

物理信息神经网络 $f(t,x)$ 可以使用 Python 代码形式为

def f(t, x):
    u = u(t, x)
    u_t = tf.gradients(u, t)[0]
    u_x = tf.gradients(u, x)[0]
    u_xx = tf.gradients(u_x, x)[0]
    f = u_t + u*u_x - (0.01/tf.pi)*u_xx
    return f

同时定义了损失函数为如下公式，这是很简单的损失函数设置，只考虑了

$$MSE=MSE_{u}+MSE_{f},\\ MSE_{u}=\frac{1}{N_{u}} \sum_{i=1}^{N_{u}}\left|u\left(t_{u}^{i}, x_{u}^{i}\right)-u^{i}\right|^{2}, \\ MSE_{f}=\frac{1}{N_{f}} \sum_{i=1}^{N_{f}}\left|f\left(t_{f}^{i}, x_{f}^{i}\right)\right|^{2} .$$

式中，$\{{t^i_u,x^i_u,u^i\}}^{N_u}_{i=1}$ 表示 $u(t,x)$ 的初始和边界训练数据, $\{{t^i_f,x^i_f\}}^{N_f}_{i=1}$ 表示 $f(t,x)$ 的内部取点。

作者使用 TensorFlow 构建并训练神经网络，具体的实现细节可参考原论文，其方法遵循了物理信息神经网络（PINN）中较为常见的损失函数设计。如果读者对此尚不熟悉，建议认真研读论文代码以加深理解。接下来的理论部分主要为 PINN 方法的原理介绍，内容较为经典，读者可快速浏览。 在实验设置方面，作者选用了 L-BFGS 优化器，构建了一个包含 9 层、每层 20 个神经元的前馈神经网络，总参数量为 3021，激活函数采用双曲正切函数（tanh）。训练过程中共采样 10000 个点，最终得到误差为$6.7×10^{−4}$的实验结果，图像如下：

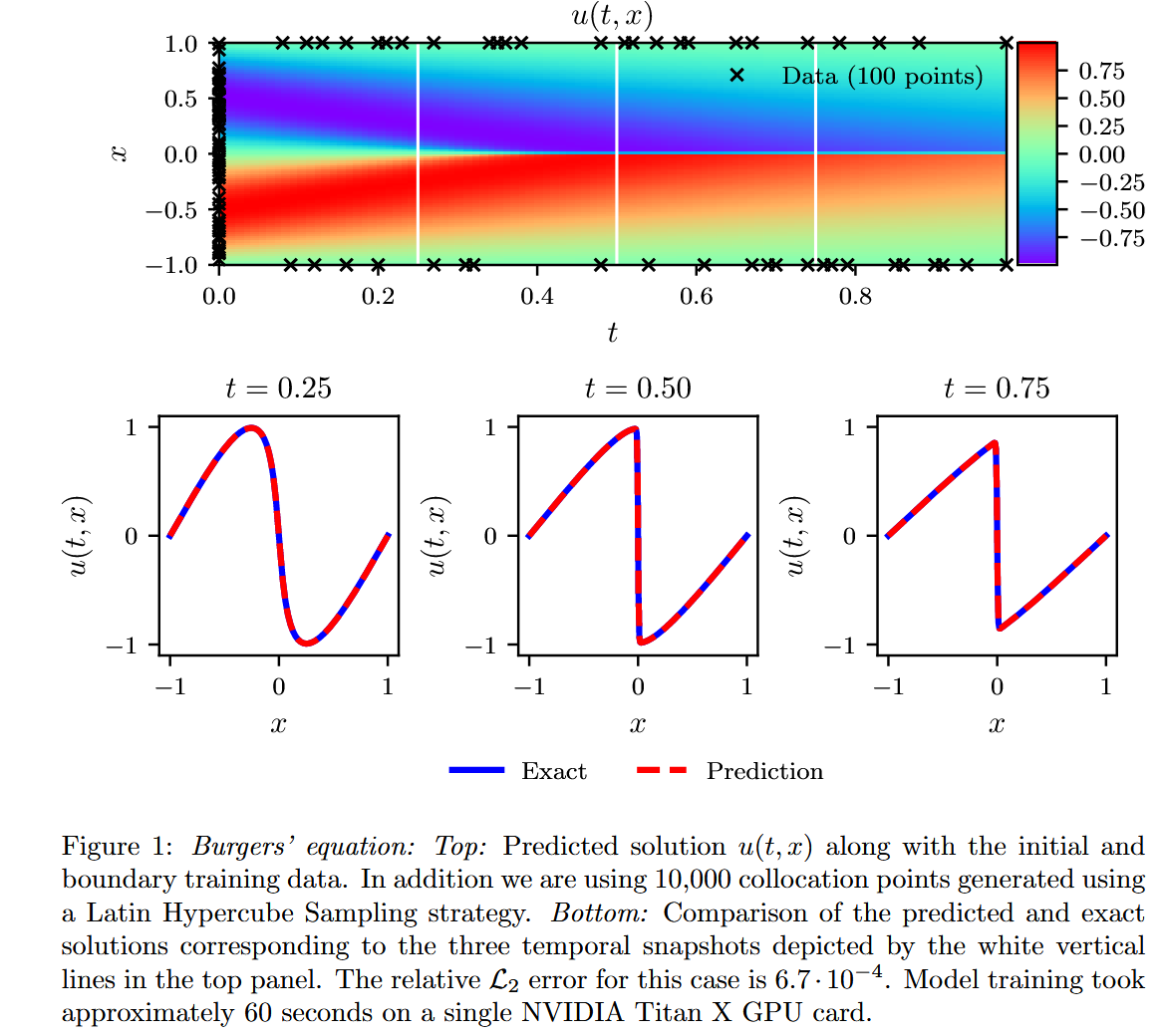
不同隐藏层数量和每层神经元数量下的相对 L2 值，而训练点和配置点的总数分别固定为 Nu = 100 和 Nf = 10,000。如预期所示，我们观察到随着层数和神经元数量的增加，误差会持续下降。

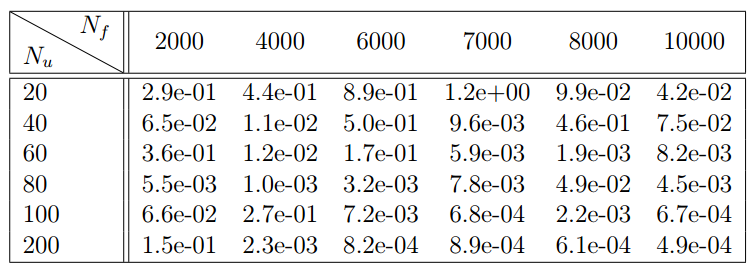
表 1：Burgers 方程：网络架构固定为 9 层，每层隐藏层包含 20 个神经元。对于不同的初始和边界训练数据 $N_u$和不同的插值点数量 $N_f$,预测解与精确解 u(t; x)之间的相 $L_2$ 误差。

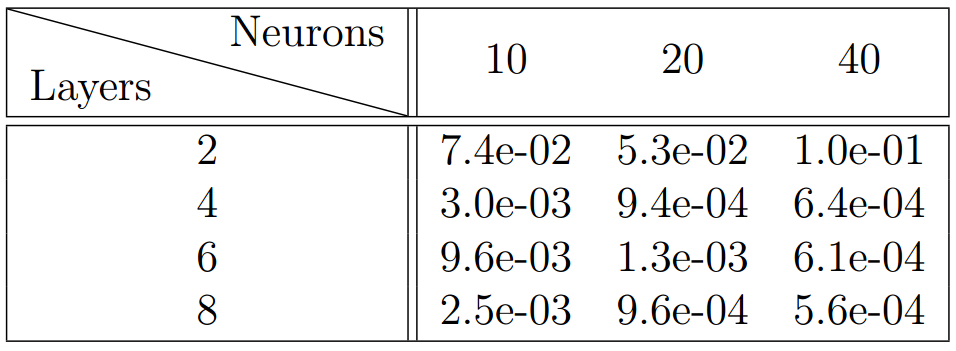
表 2：Burgers 方程：固定初始和边界训练数据 $N_u=100$和不同的插值点数量 $N_f=10000$。对于不同隐藏层数量及每层神经元数量的组合,预测解与精确解 u(t; x)之间的相 $L_2$ 误差。

Schrödinger 方程

作者使用这个例子是为了展示本文方法在处理周期性边界条件、复数解以及控制偏微分方程中不同类型非线性项的能力。

非线性的 Schrödinger 方程考虑周期边界条件下，可以写成：

$$\begin{array}{l} i h_{t}+0.5 h_{x x}+|h|^{2} h=0, \quad x \in[-5,5], \quad t \in[0, \pi / 2] \\ h(0, x)=2 \operatorname{sech}(x) \\ h(t,-5)=h(t, 5) \\ h_{x}(t,-5)=h_{x}(t, 5) \end{array}$$

其中 $h(t,x)$ 是复值解。我们定义 $f(t,x)$ 由以下公式给出：

$$f:=i h_{t}+0.5 h_{x x}+|h|^{2} h,$$

事实上，如果 $u$ 表示 $h$ 的实部， $v$ 表示 $h$ 的虚部， 那么我们可以在 $h(t,x)=[u(t,x) v(t,x)]$上多放置一个多输出的神经网络。这将得到一个多输出的神经网络 $f(t,x)$。

本文作者设计的损失函数如下：

$$M S E=M S E_{0}+M S E_{b}+M S E_{f}$$ $$M S E_{0}=\frac{1}{N_{0}} \sum_{i=1}^{N_{0}}\left|h\left(0, x_{0}^{i}\right)-h_{0}^{i}\right|^{2} \\ M S E_{b}=\frac{1}{N_{b}} \sum_{i=1}^{N_{b}}\left(\left|h^{i}\left(t_{b}^{i},-5\right)-h^{i}\left(t_{b}^{i}, 5\right)\right|^{2}+\left|h_{x}^{i}\left(t_{b}^{i},-5\right)-h_{x}^{i}\left(t_{b}^{i}, 5\right)\right|^{2}\right)\\ M S E_{f}=\frac{1}{N_{f}} \sum_{i=1}^{N_{f}}\left|f\left(t_{f}^{i}, x_{f}^{i}\right)\right|^{2} .$$

这里，$\{x_0^i,h^i_0\}^{N_0}_{i=1}$ 代表初始条件的点，$\{t^i_b\}^{N_b}_{i=1}$ 代表边界条件的点， $\{t^i_f,x^i_f\}^{N_f}_{i=1}$ 代表内部的配置点在 $f(t,x)$ 上。

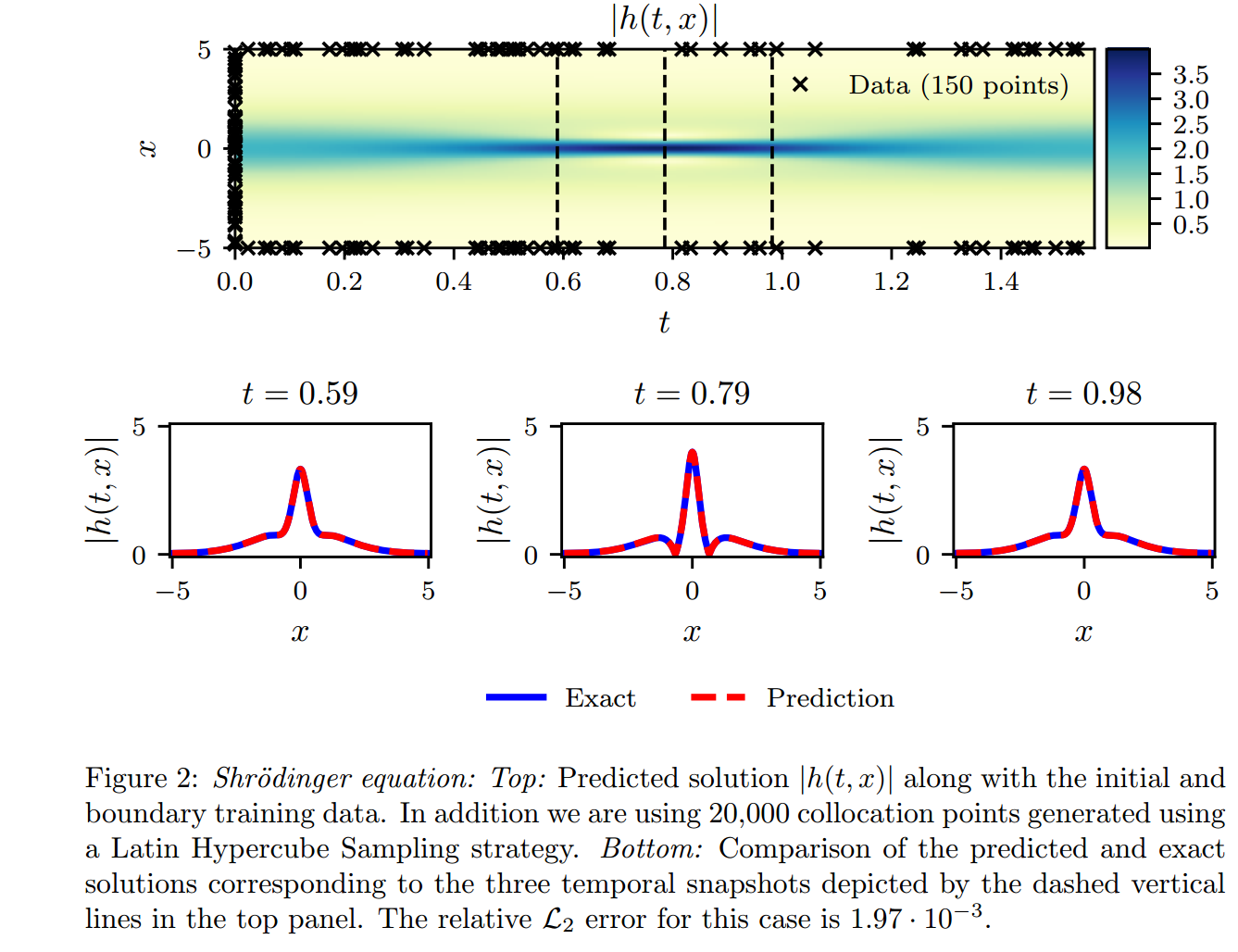
使用了通过 Latin Hypercube 采样策略生成的 20000 个共现点。底部：与顶部面板中虚线垂直线所示的三个时间快照对应的预测解与精确解的比较。此案例的相对 $L2$ 误差为 $1.97 × 10^(−3)$ 。

离散时间模型

总结

该实验在当时取得了较为优秀的结果。虽然近年来 PINN 方法的精度已有显著提升，误差已可降至极低水平，但考虑到该论文发表于 2017 年，其工作在当时仍具有代表性和参考价值。

此外，文章其他部分内容相对常规，若能够理解其中关于 Burgers 方程的实验与分析，基本上已经把握了该论文的核心思想。