RL3 Table Method

策略最简单的表示是查找表（look-up table），即表格型策略（tabular policy）。使用查找表的强化学习方法称为表格型方法（tabular method），如蒙特卡洛、Q学习和Sarsa。本章通过最简单的表格型方法来讲解如何使用基于价值的方法求解强化学习问题。（reference：https://datawhalechina.github.io/easy-rl/#/chapter3/chapter3）

基于此，本文介绍三种常用方法，Q表格（Q-table）， 时序差分（temporal difference），蒙特卡洛（MC），Sarsa

并稍微给出免模型，有模型，同策略，异策略的定义

1 免模型 (Model-free) 和 有模型 (Model-based)

1.1 Model-free

直接与环境互动，不考虑环境内的数学公式，特点是通过反复试错来改进策略，但是模拟次数需要很多

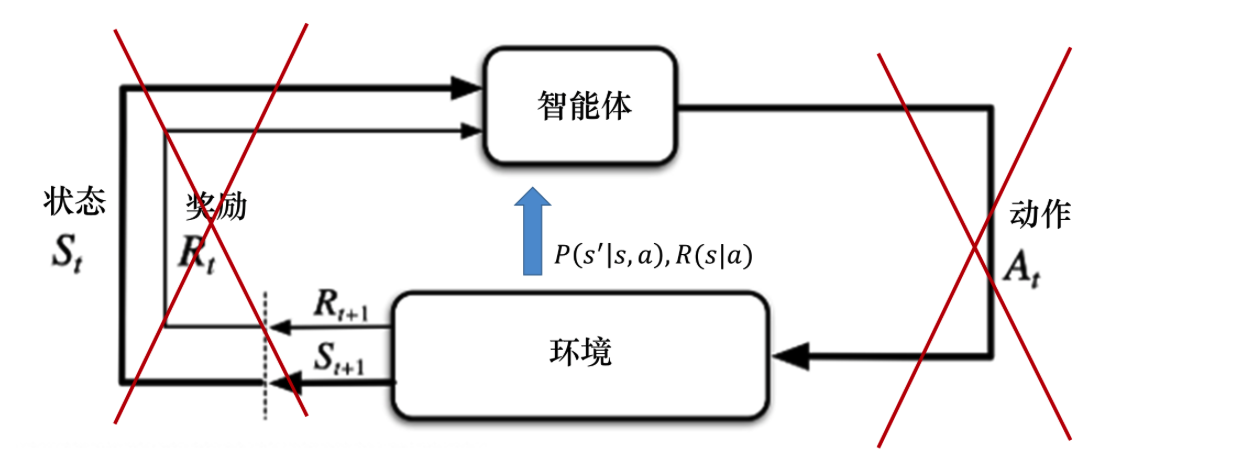
当马尔可夫决策过程的模型未知或者模型很大时，我们可以使用免模型强化学习的方法。免模型强化学习方法没有获取环境的状态转移和奖励函数，而是让智能体与环境进行交互，采集大量的轨迹数据，智能体从轨迹中获取信息来改进策略，从而获得更多的奖励。

1.2 model-based

先构建虚拟环境，在其中训练后在将模型放在真实环境中执行，特点是学习速度快（虚拟环境可以理解为概率论中的先验知识），但是极度依赖模型的准确性

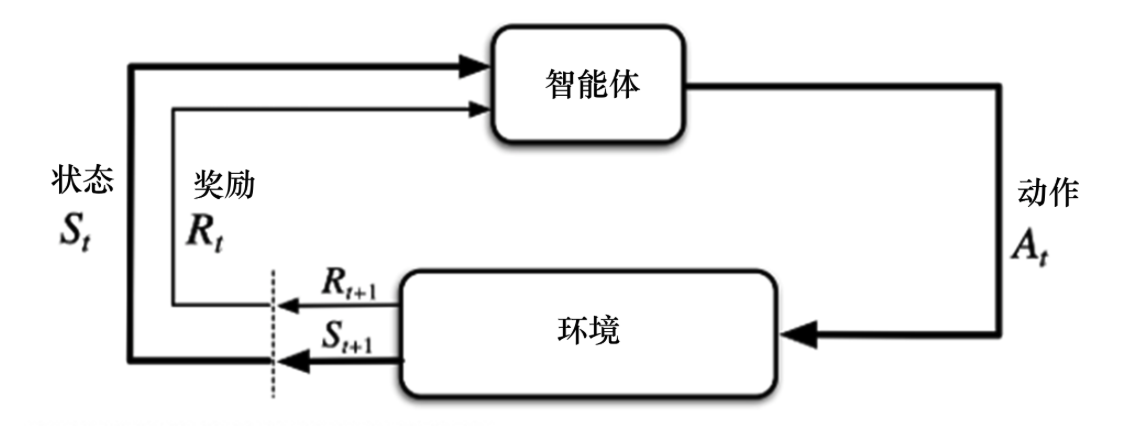
策略迭代和价值迭代都需要得到环境的转移和奖励函数，所以在这个过程中，智能体没有与环境进行交互。在很多实际的问题中，马尔可夫决策过程的模型有可能是未知的，也有可能因模型太大不能进行迭代的计算，比如雅达利游戏、围棋、控制直升飞机、股票交易等问题，这些问题的状态转移非常复杂。

2 Q表格

Q表格可以这样理解，在一个5*5的网格中，每一个网格都会记录最佳策略，当agent走到这步的时候，就可以直接通过查表的方式去决定自己的策略。其实和动态规划的思想差不多。baseline如下

动作\状态	s1	S2
a1	q_value	q_value
a2	q_value	q_value
a3	q_value	q_value

q值代表在某个状态下采取某个动作，未来预期能获得的累积奖励总和。初始化一般都可以默认为0

Q表格很好用，但是action和state很多都情况下就太大了，这就是未来会介绍到的DQN算法。当然，本文不介绍，而是介绍几种常见的计算q_value的办法

当然在此之前，我们还需要了解一下同策略和异策略

3 同策略(on-policy) & 异策略(off-policy)

本文介绍三种算法，简单说就是蒙特卡洛方法 (Monte Carlo, MC)，时序差分方法 (Temporal Difference, TD)和SARSA。其中Q-learning和SARSA都是TD的具体实现方法

4 蒙特卡洛策略评估(Monte Carlo, MC)

4.1 理论

一句话，**就是大数仿真模拟然后求平均值。**采样大量的轨迹，计算所有轨迹的真实回报，然后计算平均值。

让agent先完整的完成一个回合，然后记录下从某个状态开始到结束所拿到的所有奖励

算法流程

1. 采样：从状态s采取动作a开始，直到结束或epochs用完
2. 计算$G_t$: 计算回报
3. 更新表格的Q_value：有两种形式

$$Q(s,a) = \frac{所有局数的总回报和}{访问次数} \\ Q(s,a) \leftarrow Q(s, a) + \alpha(G_t - Q(s,a))$$

第一个很简单，直接平均就ok了，第二个是增量更新法，也是最常用的一种办法，

$\alpha$是学习率，$(G_t - Q(s,a)$是误差，决定其收敛，大于0说明鼓励这个动作，小于0说明惩罚这个动作

4.2 例子

4.2.1 设定

假设存在这样的一个迷宫

起点	空地
陷阱	终点

Reward：到达终点+10，陷阱-10，移动一步-1

$\gamma = 1, \alpha=0.5$,使用增量更新法，init all q_value in Q table are 0

4.2.2 计算

只模拟三步

局数	路径	Gt计算	Q表更新
1	(1,1) -> (2,1)	-1 + -10 =-11	Q((1,1), 下)
2	(1,1) -> (1,2) -> (2, 2)	-1 + 10 =9 -1 - 1 + 10 = 8	Q((1,2), 下) Q((1,1), 右)
3	(1,1) -> (1,2) -> (1,1) -> (2,2)	-1 * 4 + 10 =6	Q((1,1), 右)

如果是Q table的话，就是这样的

a\s	(1, 1)	(1, 2)	(2, 1)	(2, 2)
上	？	？	？	？
下	？	？	？	？
左	？	？	？	？
右	？	？	？	？

如果遇见一个坐标是之前计算过的，务必不要忘记使用增量更新法

5 时序差分（Temporal Difference, TD）

依旧是一种填表的方法，不同的是TD不需要等一局结束（不需要注意$G_t$）每走n不就更新一次Q表（也就是TD(n)）

5.1 TD(0)

5.1.1 理论

以最简单的TD（0）为例，核心公式为

$$V(s_t) \leftarrow V(s_t) + \alpha[r_{t+1} + \gamma V(s_{t+1})-V(s_t)]$$

$V(s_t)$为目前（最好的翻译是以前）这个格子的分数（旧预测），$r_{t+1} + \gamma V(s_{t+1})-V(s_t)$就是TD目标（TD target）

**时序差分误差（TD error）**就是$\delta = R_{s'} + \gamma V(s') - V(s)$,可以用更新$V(s)$来逼近真实的回报

5.1.2 例子

还是以迷宫为例，只不过这次初始化的是V Table

局数	路径	TD error	V值
1	(1, 1) -> (2, 1)	-1 + 1*0 - 0 = -1	V(1,1) = -0.5
2	(1,1) -> (1,2) -> (2, 2)	step1: -1 + 1*0 - (-0.5) = -0.5 step2: -1+10 - 0 = 9	step1: V(1, 1) = -0.5 + 0.5(-0.5) =-0.75 step2: V(1, 2) = 0 +0.5(9) = 4.5
3	(1, 1) -> (1,2) -> (2, 2)	step1: -1 +1*4.5 - (-0.75) =4.25 step2: -1+10-4.5=4.5	step1: V(1,1) = -0.75 + 0.5(4.25)=1.375 step2: V(1,2) = 4.5+0.5(4.5)=6.75

V值在确定TD error的情况下，可以直接简化计算，即$V(s_t) = V(s_t) + \gamma \delta$

此处还需要引入一个重要概念，V表是有局限性的，尤其是针对model-free的情况，因为V表没有动作a，意思就是不知道应该如何计算状态转移概率$p(s_{t+1}|s_t,a)$，所以这不是一种Q-Table的传统算法。当然，后续的Q-learning和SARSA就是两种计算V表然后再计算Q表的算法了

6. 广义策略迭代 (Generalized Policy Iteration, GPI)

为什么需要广义策略迭代？因为在不知道$P(s' \mid s, a)$和$R(s, a)$的情况下，即便算出了$V(s)$,也无法推导出最优动作，（公式如下，方便理解）

$$Q_\pi(s,a) = R(s,a) + \gamma \sum_{s' \in S}P(s' \mid s,a)V_\pi(s')$$

此时就需要使用到GPI，广义策略迭代是指策略评估 (Policy Evaluation)和策略改进 (Policy Improvement)这两个过程相互作用、不断迭代的过程。

Evaluation根据当前策略$\pi$来估算价值函数（$V$或$Q$）

Improvement是指，得到价值函数后，通过“贪心”的方法改进策略，使其朝着更优的方向演变

对策略评估部分进行修改，使用蒙特卡洛的方法代替动态规划的方法估计 Q 函数。我们首先进行策略评估，使用蒙特卡洛方法来估计策略$Q=Q_\pi$，然后进行策略更新，即得到 Q 函数后，我们就可以通过贪心的方法去改进它

$$\pi(s) = argmaxQ(s,a)$$

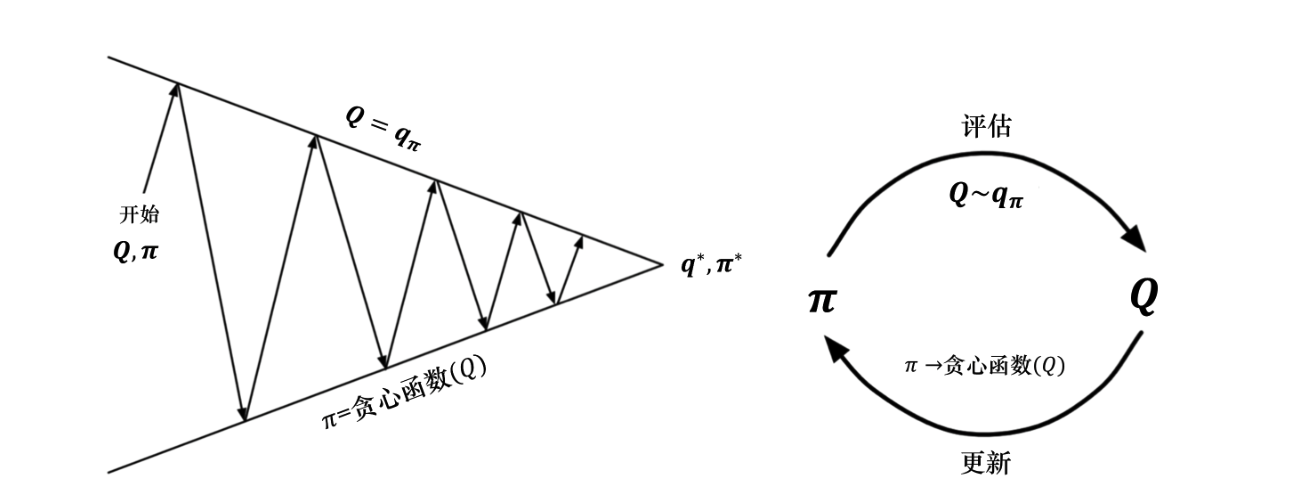
最好的该改进点是，在之前，只要不知道P和R，求出V也没用。但现在可以直接评估Q函数（通过Q表），直接选取Q值最大的动作

有两种方案：

A：MC探索

B：e-贪心搜索

6. SARSA

6.1 理论

先说定义：Sarsa 是一种**同策略（on-policy）**算法，它优化的是它实际执行的策略，它直接用下一步会执行的动作去优化 Q 表格。同策略在学习的过程中，只存在一种策略，它用一种策略去做动作的选取，也用一种策略去做优化。所以 Sarsa 知道它下一步的动作有可能会跑到悬崖那边去，它就会在优化自己的策略的时候，尽可能离悬崖远一点。这样子就会保证，它下一步哪怕是有随机动作，它也还是在安全区域内。

SARSA不同于前文讲的那些，是直接作用于$Q(s,a)$的，其计算公式为

$$Q(s,a) \leftarrow Q(s,a) + \alpha[r_{t+1} + \gamma Q(s_{t+1},a_{t+1})-Q(s,a)]$$

是不是很想前文的TD？这就是照搬了思路而已，当然该公式只是策略评估，对于策略改进，我们需要使用$\epsilon-greedy$

6.2 例子

依旧迷宫，当然此处假设$\epsilon=0.1$（90%选分最高的，10%瞎跑）

Step1（s） 策略改进（决定这么走）

从s1出发，应该附近都是0，所以通过$\epsilon-greedy$随机选择了一个动作向右，此时的状态动作为(s1, 右边)

Step2（a，r） 执行与观测

agent往右走并进入了空地s2，获取了奖励$r=-1$

Step3（s‘） 再次策略改进（SARSA）

在更新s1的分数之前，先决定在s2应该怎么走，发现目前Q表也是0，于是通过$\epsilon-greedy$决定向下走

Step4（a’，Q）策略评估

利用前几步，带入公式

$$Q(s_1, 右) \leftarrow Q(s_1, 右) + 0.5[-1+1 \times Q(s_2, 下)-Q(s_1, 右)]$$

此时更新好了全新的$Q(s_1, 右)$，依旧进行n轮迭代得到最终解

6.3 总结

用TD的方法（计算Q）+$\epsilon-greedy$更新策略，就得到了SARSA，这个算法的本身就是$s,a,r,s',a'$

7. Q学习（Q-learning）

7.1 理论

和SARSA差不多，只是稍微变了一下Q值更新策略，首先列出公式

$$Q(s,a) \leftarrow Q(s,a) + \alpha[r_{t+1} + \gamma \max_{a}Q(s_{t+1},a_{t})-Q(s,a)]$$

TD target发生了变化

7.2 实验

和SARSA一样，不同点在于step4，更新评估部分

$\epsilon-greedy$在确定动作之后，比如$(s_2, 左)$,SARSA就会用$(s_2, 左)$的值带入公式计算新Q值，而Q-learning会不管$\epsilon-greedy$的结果，直接选择附近的最高Q值，即在填表时只选最高的走，以追求最优解

8. 同策略与异策略

Sarsa 是一个典型的同策略算法，它只用了一个策略$\pi$，它不仅使用策略$\pi$学习，还使用策略$\pi$与环境交互产生经验。 如果策略采用$\epsilon-greedy$，它需要兼顾探索，为了兼顾探索和利用，它训练的时候会显得有点“胆小”。它在解决悬崖行走问题的时候，会尽可能地远离悬崖边，确保哪怕自己不小心探索了一点儿，也还是在安全区域内。此外，因为采用的是，$\epsilon-greedy$策略会不断改变（$\epsilon$值会不断变小），所以策略不稳定。

Q学习是一个典型的异策略算法，它有两种策略————目标策略和行为策略，它分离了目标策略与行为策略。Q学习可以大胆地用行为策略探索得到的经验轨迹来优化目标策略，从而更有可能探索到最佳策略。行为策略可以采用 εε-贪心 算法，但目标策略采用的是贪心算法，它直接根据行为策略采集到的数据来采用最佳策略，所以 Q学习 不需要兼顾探索。

我们比较一下 Q学习 和 Sarsa 的更新公式，就可以发现 Sarsa 并没有选取最大值的最大化操作。因此，Q学习是一个非常激进的方法，它希望每一步都获得最大的利益；Sarsa 则相对较为保守，它会选择一条相对安全的迭代路线。

总结

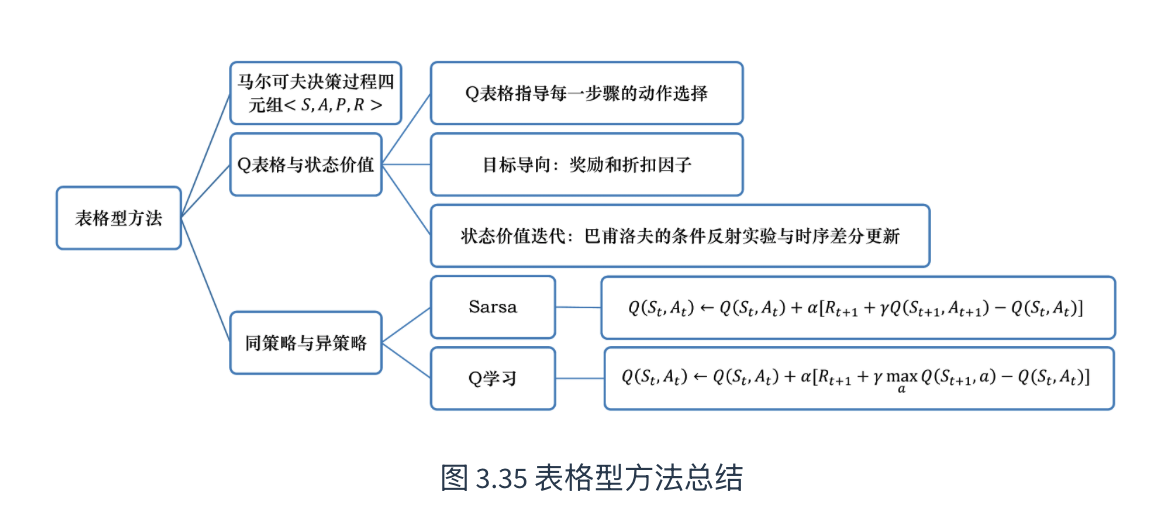
8. 一些定义

**自举（Bootstrapping）**是指在更新当前状态或动作的价值时，不等待最终的真实回报，而是直接利用对后续状态价值的“现有估计值”来更新当前的“估计值”