DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators

这是一篇开山之作提出了一个深度学习框架 DeepONet 用于求解偏微分方程的求解器，这篇论文介绍了原理。

摘要

摘要原文：

While it is widely known that neural networks are universal approximators of continuous functions, a less known and perhaps more powerful result is that a neural network with a single hidden layer can approximate accurately any nonlinear continuous operator [5]. This universal approximation theorem is suggestive of the potential application of neural networks in learning nonlinear operators from data. However, the theorem guarantees only a small approximation error for a sufficient large network, and does not consider the important optimization and generalization errors. To realize this theorem in practice, we propose deep operator networks (DeepONets) to learn operators accurately and efficiently from a relatively small dataset. A DeepONet consists of two sub-networks, one for encoding the input function at a fixed number of sensors $x_i = 1, ... , m$ (branch net), and another for encoding the locations for the output functions (trunk net). We perform systematic simulations for identifying two types of operators, i.e., dynamic systems and partial differential equations, and demonstrate that DeepONet significantly reduces the generalization error compared to the fully-connected networks. We also derive theoretically the dependence of the approximation error in terms of the number of sensors (where the input function is defined) as well as the input function type, and we verify the theorem with computational results. More importantly, we observe high-order error convergence in our computational tests, namely polynomial rates (from half order to fourth order) and even exponential convergence with respect to the training dataset size.

摘要翻译：

尽管神经网络是连续函数的通用逼近器这一事实广为人知，但一个较少为人所知且可能更强大的结果是：具有单个隐藏层的神经网络能够精确逼近任何非线性连续算子。这一通用逼近定理暗示了神经网络在从数据中学习非线性算子方面的潜在应用。然而，该定理仅保证在网络规模足够大时存在较小的逼近误差，并未考虑重要的优化误差和泛化误差。为了在实践中实现这一定理，我们提出**深度算子网络（DeepONets）**以从相对较小的数据集准确高效地学习算子。一个 DeepONet 由两个子网络组成：一个用于在固定数量的传感器上编码输入函数 $x_i = 1, ..., m$（分支网络），另一个用于编码输出函数的位置（主干网络）。我们通过系统性模拟识别两种类型的算子，即动态系统和偏微分方程，并证明 DeepONet 相较于全连接网络显著降低了泛化误差。我们还从理论上推导了近似误差与传感器数量（即输入函数定义的传感器数量）以及输入函数类型之间的依赖关系，并通过计算结果验证了该定理。更重要的是，我们在计算测试中观察到高阶误差收敛，即多项式收敛率（从半阶到四阶）甚至与训练数据集大小相关的指数收敛。

讨论

这篇论文首先构建两个子网络，分别对输入函数和位置变量进行编码，然后将它们合并以计算输出。随后在四个常微分方程和偏微分方程问题上测试了DeepONets，并且展示了通过这种归纳偏置，DeepONets 能够实现较小的泛化误差。他们还系统的研究了不同因素对测试误差的影响，包括传感器数量、最大预测时间、输入函数空间的复杂性、训练数据集大小和网络规模。

这篇文章也有对未来的展望，包括两个展望：

• 展望 a)：尚未有关于网络规模对算子近似的理论结果，类似于函数近似的宽度和深度界限 [10]。我们还尚未理论上理解 DeepONets 为什么能够引起较小的泛化误差。

• 展望 b)：本文中使用了全连接神经网络作为两个子网络，但正如我们在 2.1 节中讨论的，我们还可以使用其他网络架构，如卷积神经网络或 “注意力” 机制。这些修改可能进一步提高 DeepONets 的准确性。

实验

考虑一个一维的常微分方程：

$$\frac{ds(x)}{dx} = g(s(x),u(x),x), x\in[0,1]$$

初始条件为 $s(0)=0$。目标是为任意的 u(x)预测整个区间的 $[0,1]$ 上的 $s(x)$。

线性案例： $g(s(x),u(x),x)=u(x)$

首先通过选择 $g(s(x),u(x),x)=u(x)$ 来考虑一个线性问题，这相当于学习反导数算子 (antiderivative operator):

$$G:u(x) \mapsto s(x) = \int_{0}^{x} u(\tau)d\tau$$

为了获得 FNNs 的最佳性能，我们对三个超参数进行网格搜索：深度从 2 到 4，宽度从 10 到 2560，学习率从 0.0001 到 0.01。学习率为 0.01、0.001 和 0.0001 时测试数据集的均方误差（MSE）如下图所示：

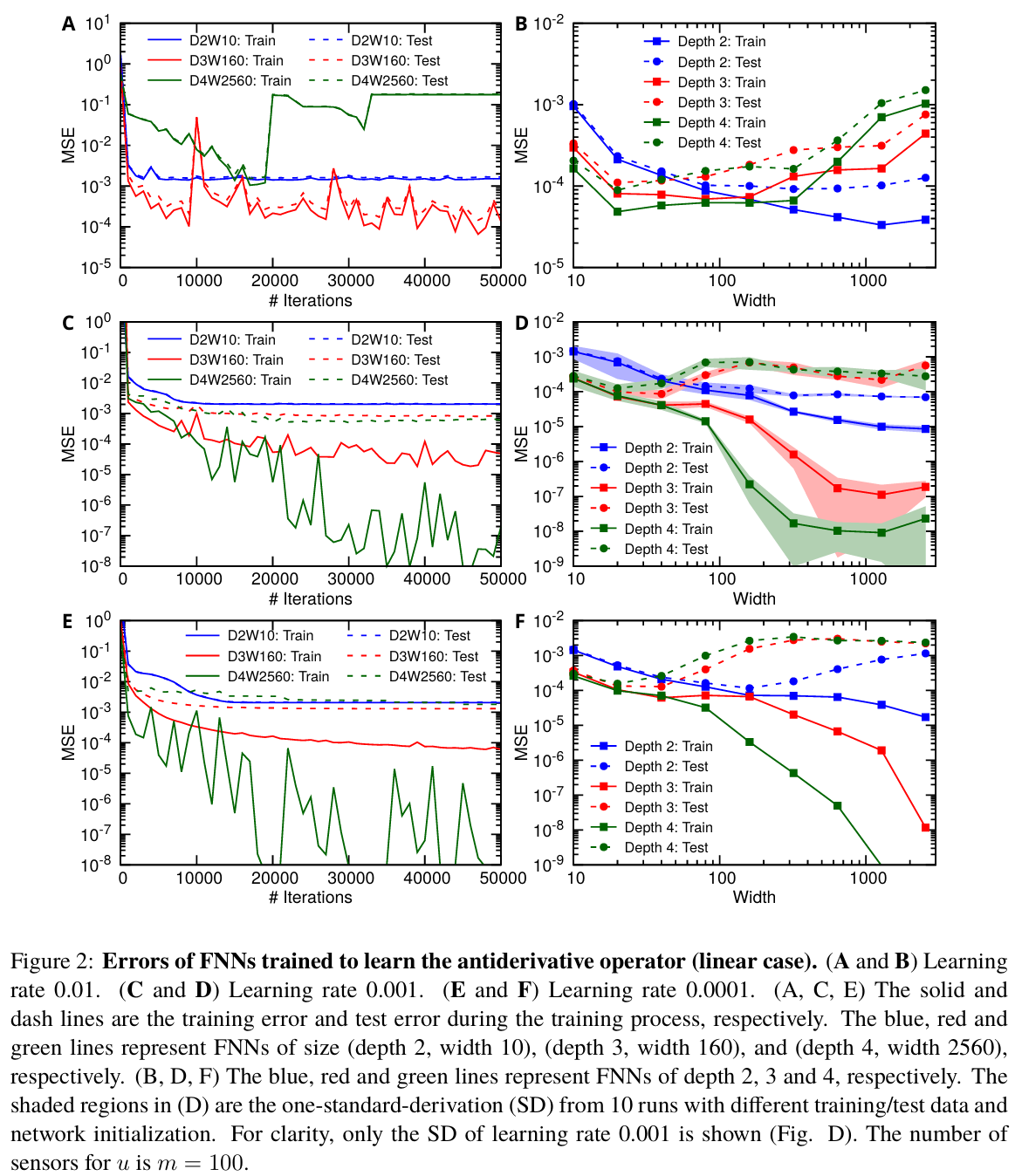
上面实验表明：只选择了深度最多为 4，但结果表明进一步增加深度并不能改善误差。在所有这些超参数中，最小的测试误差约为 $10^{-4}$ ，该网络的深度为 2，宽度为 2560，学习率为 0.001。得到结论为当网络较小时，训练误差较大，泛化误差（测试误差与训练误差之间的差异）较小，这是由于表达能力有限。当网络规模增加时，训练误差减少，但泛化误差增加。

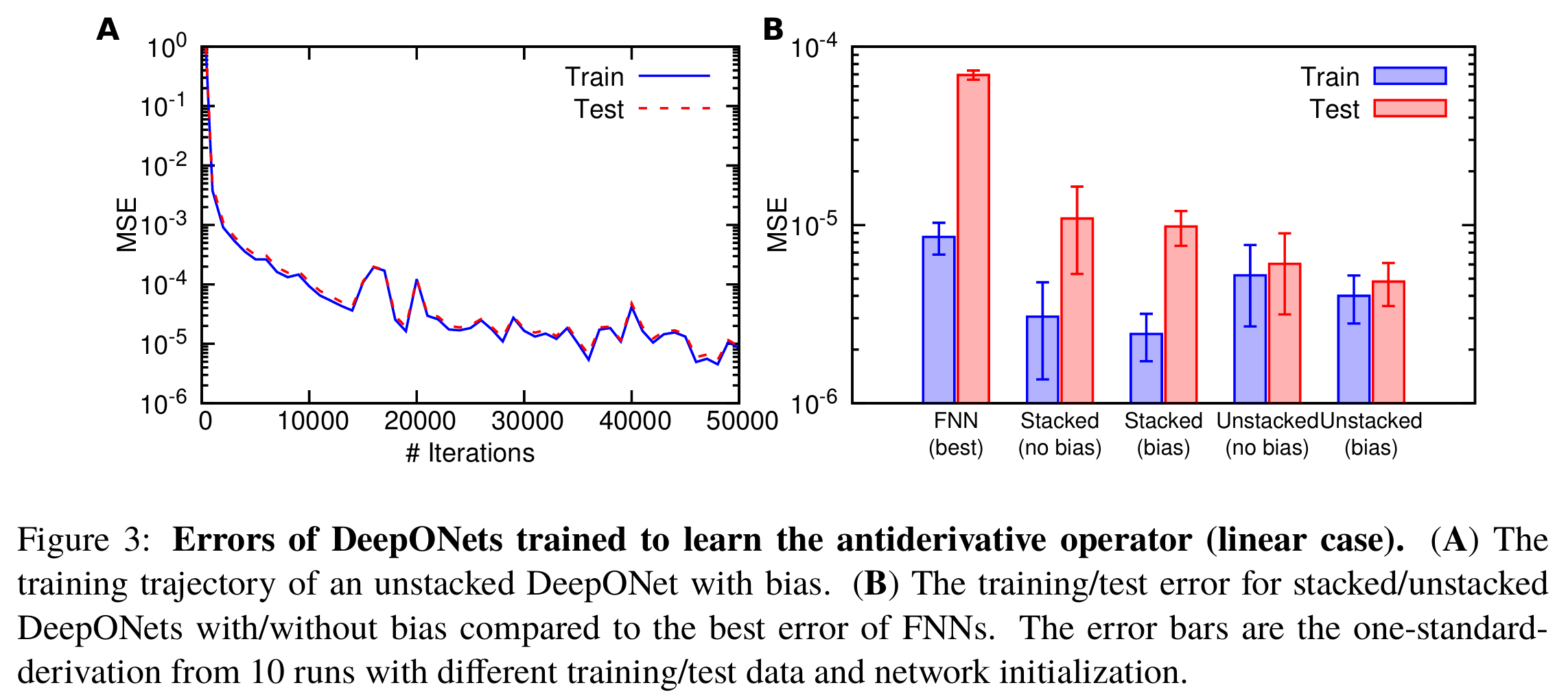
与 FNNs 相比，DeepONets 具有更小的泛化误差，从而具有更小的测试误差。这里我们不打算找到最佳超参数，只测试表 2 中列出的两个 DeepONets 的性能。图 3A 显示了带有偏置的非堆叠 DeepONet 的训练轨迹，泛化误差可以忽略不计。我们观察到，

• 对于堆叠和非堆叠的 DeepONets，向分支网络和公式 (2) 中添加偏置减少了训练和测试误差（图 3B）；带有偏置的 DeepONets 也具有较小的不确定性，即从随机初始化训练时更加稳定（图 3B）。

• 与堆叠 DeepONets 相比，尽管非堆叠 DeepONets 具有较大的训练误差，但测试误差较小，这是由于较小的泛化误差。因此，带有偏置的非堆叠 DeepONets 达到了最佳性能。

• 此外，非堆叠 DeepONets 的参数数量少于堆叠 DeepONets，因此可以使用更少的内存更快地进行训练。

非线性案例： $g(s(x),u(x),x) = −s^2(x)+u(x)$

接下来，这篇文章考虑一个非线性问题：

$$g(s(x),u(x),x) = −s^2(x)+u(x)$$

因为对于某些 $u(x),s(x)$ 可能会发散，我们通过去除最差的 $1$ 预测来计算测试 MSE。在网络训练过程中，堆叠和非堆叠 DeepONets 的训练 MSE 和测试 MSE 都在减少，但非堆叠 DeepONets 的训练 MSE 和测试 MSE 之间的相关性更紧密（图 4A），即泛化误差较小。这种紧密的相关性在多次随机训练数据集和网络初始化的运行中也能观察到（图 4B）。此外，非堆叠 DeepONets 的测试 MSE 和训练 MSE 几乎呈现线性相关性：

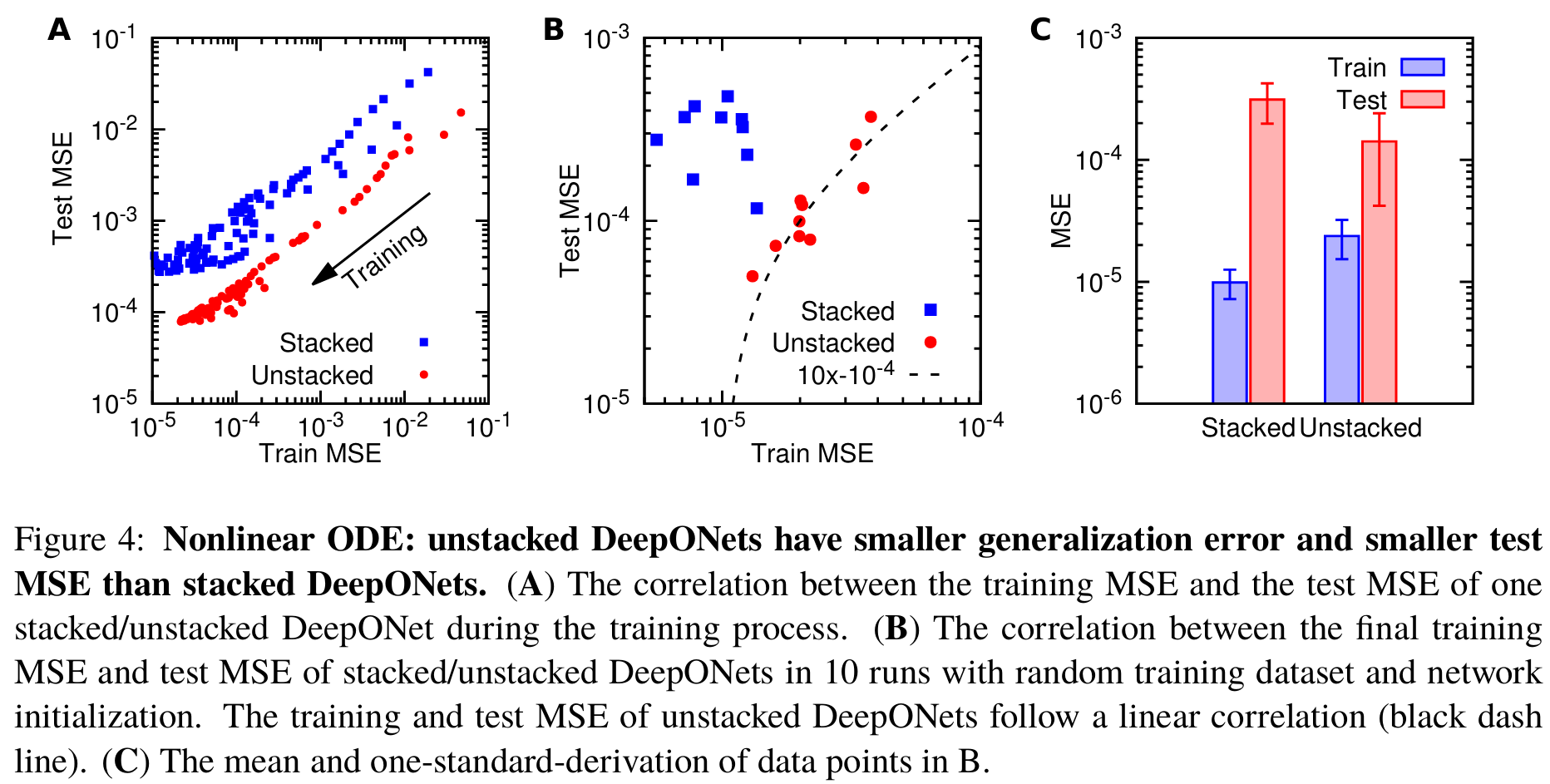
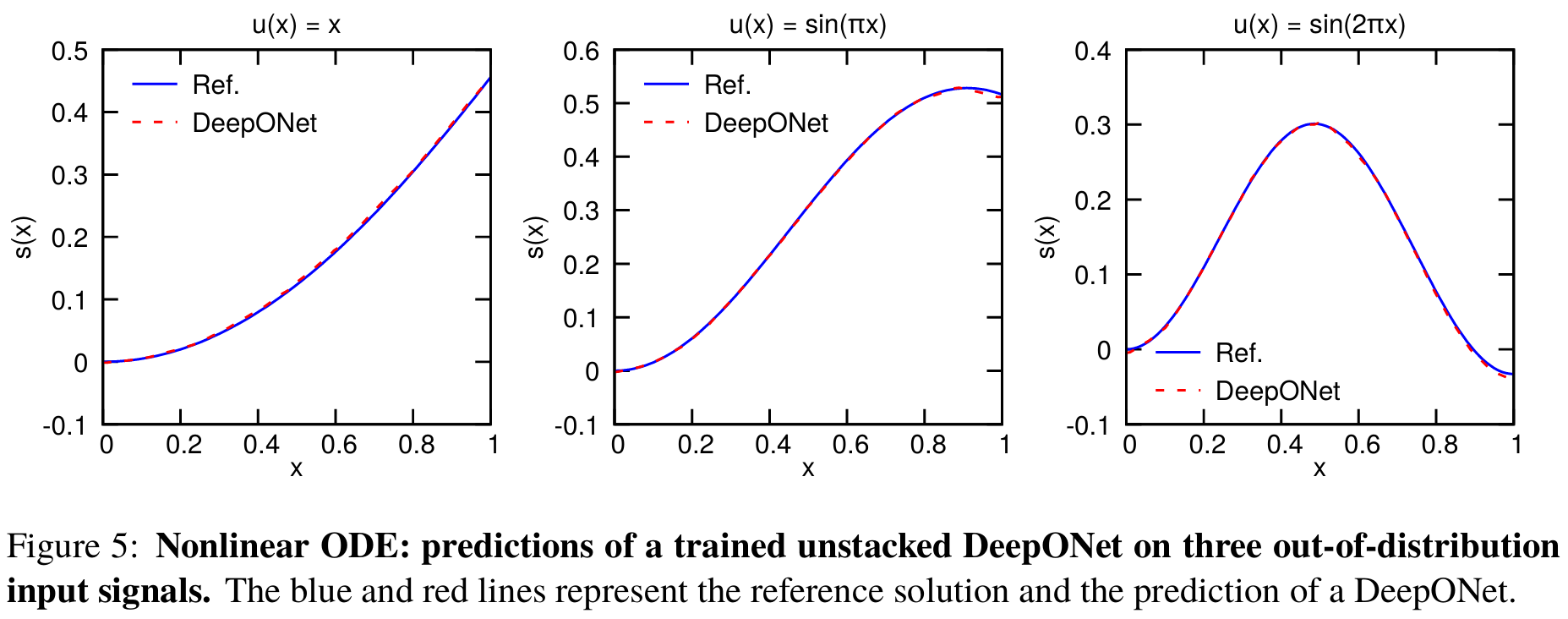
图 4C 显示，由于较小的泛化误差，非堆叠 DeepONets 具有较小的测试 MSE。DeepONets 即使在分布外预测中也能工作，参见图 5 中的三个预测示例。在接下来的研究中，我们将使用非堆叠 DeepONets。

$$MSE_{test} \approx 10 × MSE_{train} - 10^{-4}$$

图 4C 显示，由于较小的泛化误差，非堆叠 DeepONets 具有较小的测试 MSE。DeepONets 即使在分布外预测中也能工作，参见图 5 中的三个预测示例。在接下来的研究中，我们将使用非堆叠 DeepONets。

受外力作用的重力摆

略

方法

深度算子网络（DeepONets）

我们专注于在更一般的设置中学习算子，其中对训练数据集的唯一要求是输入函数的传感器 ${x_1,x_2,...,x_m}$ 的一致性。在这种一般设置中，网络输入由两个独立的组件组成：$[u(x_1), u(x_2), ..., u(x_m)]^T$ 和 $y$（图 1A），目标是通过设计网络架构来获得良好的性能。一种直接的解决方案是直接采用经典网络，如 FNN、CNN 或 RNN，并将两个输入拼接在一起作为网络输入，即 $[u(x_1), u(x_2), ..., u(x_m), y]^T$。然而，该输入没有任何特定结构，因此选择 CNN 或 RNN 等网络没有意义。在这里，我们使用 FNN 作为基准模型。

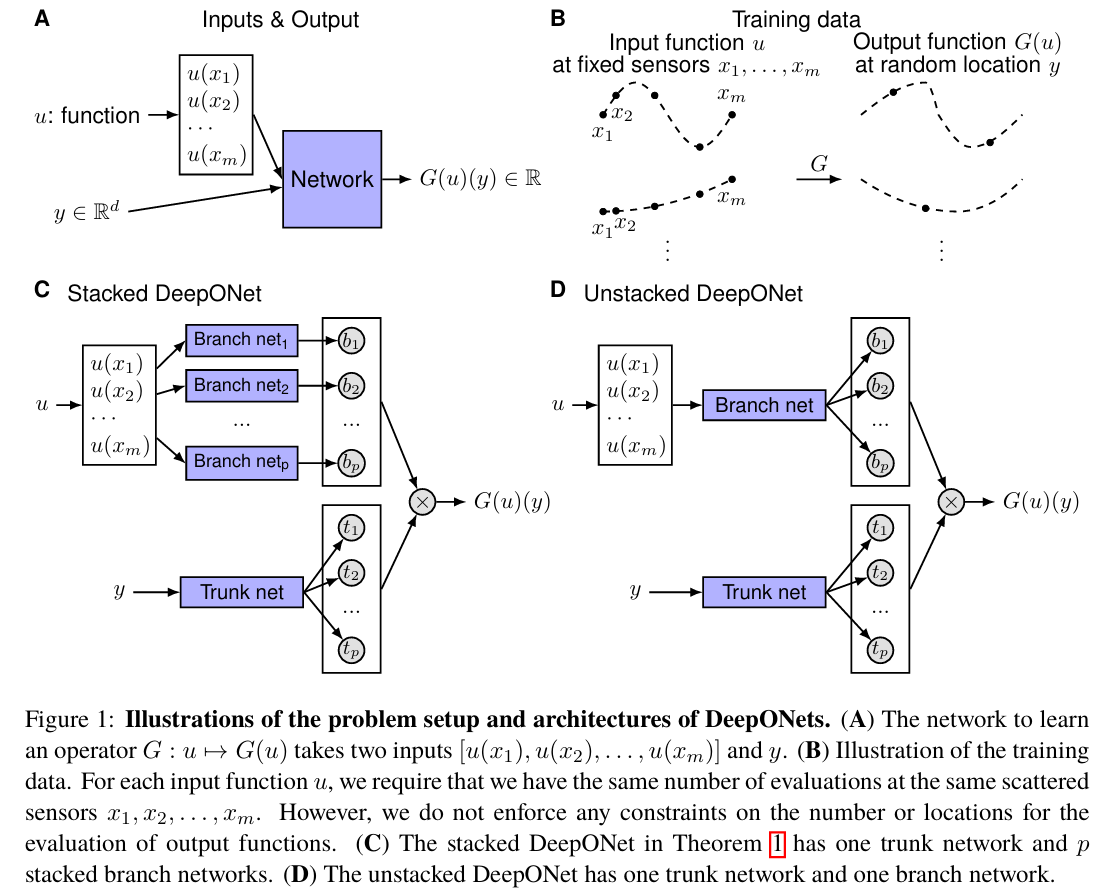
在高维问题中，$y$ 是一个具有 $d$ 个分量的向量，所以 $y$ 的维度与 $u(x_i),i = 1, 2,...,m$ 的维度不匹配。这也阻止了我们将 $u(x_i)$ 和 $y$ 同等对待，因此需要至少两个子网络来分别处理 $[u(x_1), u(x_2), ..., u(x_m)]^T$ 和 $y$ 。尽管通用逼近定理（定理 1）没有对总误差提供任何保证，但它仍为我们提供了一个网络结构（方程 1）。定理 1 仅考虑了一个具有单隐藏层的浅层网络，因此我们将其扩展到具有更强表现力的深层网络。我们提出的架构如图 1C 所示，具体细节如下。首先有一个 “主干” 网络，它以 $y$ 为输入并输出 $[t_1, t_2, ..., t_p]^T \in R^p$。除了主干网络，还有 p 个 “分支” 网络，每个网络以 $[u(x_1), u(x_2), ..., u(x_m)]^T$ 为输入并输出一个标量 $b_k \in R, k = 1, 2, ..., p$ 。我们将它们合并如方程 1：

$$G(u)(y) \approx \sum^p_{k=1} b_kt_k,$$

我们注意到主干网络在最后一层也应用了激活函数，即 $t_k = ξ(⋅)$ 对于 $k = 1,2,...,p$，因此这种主干-分支网络也可以被看作是一个主干网络，其最后一层的每个权重由另一个分支网络参数化，而不是经典的单变量。我们还注意到，在方程 1 中，每个 $b_k$ 分支网络的最后一层没有偏置。尽管在定理 1 中偏置不是必要的，但添加偏置可能通过减少泛化误差来提高性能。除了在分支网络中添加偏置外，我们还可以在最后阶段添加一个偏置 $b_0 \in R$：

$$G(u)(y) \approx \sum^p_{k=1} b_kt_k+b_0,$$

在实践中，p 至少是 10 的数量级，使用大量分支网络在计算和内存上都很昂贵。因此，我们将所有分支网络合并为一个单一的分支网络（图 1D），即单一分支网络输出一个向量 $[b_1, b_2, ..., b_p]^T \in R_p$。在第一个 DeepONet（图 1C）中，有 p 个并行堆叠的分支网络，因此我们称其为“堆叠 DeepONet”，而我们称第二个 DeepONet（图 1D）为 “非堆叠 DeepONet”。所有版本的 DeepONet 都在 DeepXDE 中实现，这是一个用户友好的 Python 库，专为科学机器学习设计。

DeepONet 是一种高级网络架构，没有定义其内部主干和分支网络的架构。为了单独展示 DeepONet 的能力和良好性能，我们选择最简单的 FNN 作为本研究中子网络的架构。使用卷积层可能会进一步提高准确性。然而，卷积层通常适用于传感器 ${x_1,x_2,...,x_m}$ 分布在等间距网格上的方形域，因此作为替代方案并针对更一般的设置，我们可以使用 “注意力” 机制。

在神经网络架构中融入一些先验知识通常会诱导出良好的泛化能力。这种归纳偏差在许多网络中得到了体现，例如用于图像的 CNN 和用于序列数据的 RNN。DeepONet 即使使用 FNN 作为其子网络也能取得成功，这也归功于其强大的归纳偏差。输出 $G(u)(y)$ 有两个独立的输入 $u$ 和 $y$，因此显式使用主干和分支网络与这种先验知识是一致的。更广泛地说，$G(u)(y)$ 可以被看作是在 $u$ 条件下的 $y$ 的函数。找到一种有效的方法来表示条件输入仍然是一个开放的问题，并且已经提出了不同的方法，例如特征变换。

数据生成

进程的输入信号 $u(x)$ 在系统识别中起着重要作用。显然，输入信号是影响进程以收集其响应信息的唯一可能性，识别信号的质量决定了任何模型在最佳情况下所能达到的准确度上限。在本研究中，我们主要考虑两个函数空间：高斯随机场（Gaussian random field，GRF）和正交（Chebyshev）多项式。

我们使用均值为零的 GRF：

$$u \sim \mathcal{G}\left(0, k_{l}\left(x_{1}, x_{2}\right)\right)\\ k_{l}\left(x_{1}, x_{2}\right)=\exp \left(-\left\|x_{1}-x_{2}\right\|^{2} / 2 l^{2}\right)$$

其中协方差核 $k_l$ 是具有长度尺度参数 $l>0$ 的径向基函数（radial-basis function，RBF）核。长度尺度 $l$ 决定了采样函数的平滑度，较大的 $l$ 导致平滑度更高的 $u$。

设 $M>0$ 且 $T_i$ 是第一类切比雪夫多项式。我们将 $N$ 次正交多项式定义为：

$$V_{\mathrm{poly}}=\left\{\sum_{i=0}^{N-1} a_{i} T_{i}(x):\left|a_{i}\right| \leq M\right\}$$

我们通过从 $[−M,M]$ 中随机采样 $a_i$ 来生成 $u$ 的样本，从而从 Vpoly 中生成数据集。

从选择的函数空间中采样 $u$ 后，我们通过 $Runge-Kutta (4, 5)$ 方法求解 $ODE$ 系统，通过二阶有限差分法求解 PDE，以获得参考解。我们注意到一个数据点是一个三元组 $(u, y, G(u)(y))$，因此一个特定的输入 $u$ 可能在多个数据点中出现，但 $y$ 的取值不同。例如，一个大小为 $10000$ 的数据集可能仅由 $100$ 条 $u$ 轨迹生成，每条轨迹在 $100$ 个 $y$ 位置上评估 $G(u)(y)$。

识别非线性动态系统的传感器数量

在本节中，我们研究了需要多少个传感器点才能达到识别非线性动态系统的精度 $\epsilon$ 。假设动态系统受以下 ODE 系统约束：

$$\begin{cases} \frac{d}{dx}s(x)=g(s(x),u(x),x), \\ s(a)=s_0, \end{cases}$$

其中 $u \in V$（$C[a,b]$ 的紧子集）是输入信号，$s:[a,b] \rightarrow R^K$ 是系统（3）的解，作为输出信号。

设 $G$ 是将输入 $u$ 映射到输出 $s$ 的算子，即 $G_u$ 满足

$$(G_u)(x) = s_0 + \int_a^xg((G_u)(t),u(t),t)dt$$

现在，我们在区间 $[a,b]$ 上选择均匀的 $m+1$ 个点 $x_j = a + j(b−a)/m，j=0,1,...,m$，并定义函数 $u_m(x)$ 如下：

$$u_m(x)=u(x_j)+\frac{u(x_{j+1}-u(x_j))}{x_{j+1}-x_j}(x-x_j),x_j\le x\le x_{j+1},j=0,1,...,m-1$$

将映射 $u$ 到 $u_m$ 的算子记为 $L_m$，并设 $U_m={L_m(u)∣u\in V}$，显然这是 $C[a,b]$ 的一个紧子集，因为 $V$ 是紧集且连续算子 $L_m$ 保持紧凑性。自然地，$W_m: = V \cup U_m$ 作为两个紧集的并集也是紧的。然后，设 $W:=\cup_{i=1}^\infty W_i,$ 而定理 7 指出 $W$ 仍然是一个紧凑集。由于 $G$ 是连续算子，$G(W)$ 在 $C([a,b]; \mathbb{R}^K)$ 中是紧凑的。接下来的讨论主要在 $W$ 和 $G(W)$ 中进行。为了分析方便，我们假设 $g(s,u,x)$ 满足 $G(W) × W$ 上关于 $s$ 和 $u$ 的 Lipschitz 条件，即存在一个常数 $c > 0$，使得

$$\left\|\boldsymbol{g}\left(\boldsymbol{s}_{\mathbf{1}}, u, x\right)-\boldsymbol{g}\left(\boldsymbol{s}_{\mathbf{2}}, u, x\right)\right\|_{2} \leq c\left\|\boldsymbol{s}_{\mathbf{1}}-\boldsymbol{s}_{\mathbf{2}}\right\|_{2} \\ \left\|\boldsymbol{g}\left(\boldsymbol{s}, u_{1}, x\right)-\boldsymbol{g}\left(\boldsymbol{s}, u_{2}, x\right)\right\|_{2} \leq c\left|u_{1}-u_{2}\right|$$

请注意，这个条件很容易实现，例如，只要 $g$ 在 $G(W) × W$ 上关于 $s$ 和 $u$ 是可微分的。

对于 $u\in V , u_m \in U_m$ ,存在一个常数 $κ(m,V)$，它取决于 $m$ 和紧凑空间 $V$ ，使得

$$\max _{x \in[a, b]}\left|u(x)-u_{m}(x)\right| \leq \kappa(m, V), \quad \kappa(m, V) \rightarrow 0 \text { as } m \rightarrow \infty .$$

当 $V$ 是具有 RBF 内核的 GRF 时，$κ(m,V ) ∼ \frac{1}{m^2l^2}$，证明见附录 C。基于这些概念，我们可以得出以下定理。

总结

这是一篇非常不错的深度学习识别函数的神经网络，值得利用这个框架去做一些别的问题。