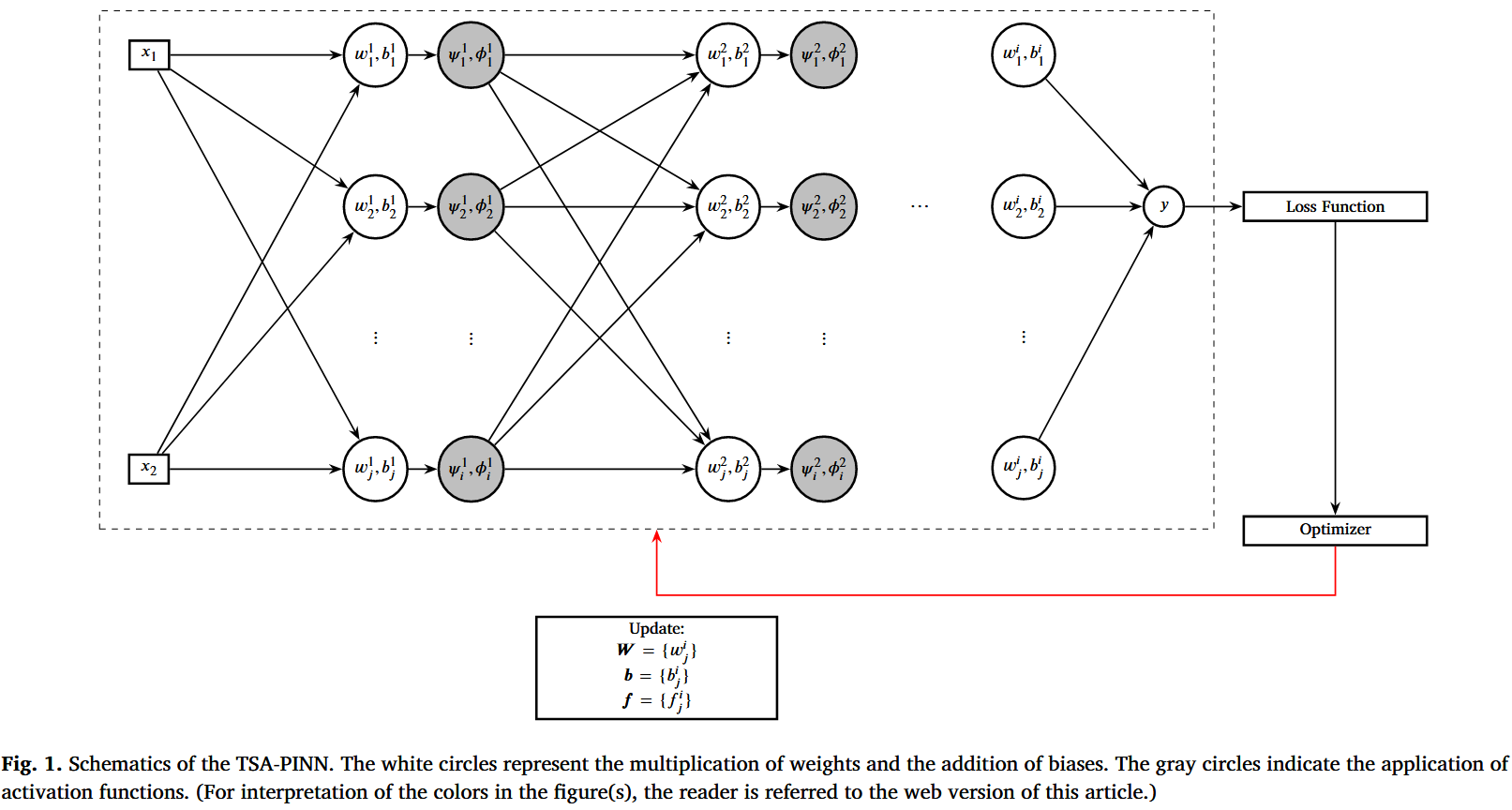
这是一篇使用 VPinn 来求解 Navier-Stokes 方程的论文。
我们先来看看这篇论文的摘要:
英文原文:
We present TSA-PINN, a novel Physics-Informed Neural Network (PINN) that leverages a Trainable Sinusoidal Activation (TSA) mechanism to approximate solutions to the Navier-Stokes equations. By incorporating neuronwise sinusoidal activation functions with trainable frequencies and a dynamic slope recovery mechanism, TSAPINN achieves superior accuracy and convergence. Its ability to dynamically adjust activation frequencies enables efficient modeling of complex fluid behaviors, reducing training time and computational cost. Our testing goes beyond canonical problems, to study less-explored and more challenging scenarios, which have typically posed difficulties for prior models. Various numerical tests underscore the efficacy of the TSA-PINN model across five different scenarios. These include steady-state two-dimensional flows in a lid-driven cavity at two different Reynolds numbers; a cylinder wake problem characterized by oscillatory fluid behavior; and two time-dependent three-dimensional turbulent flow cases. In the turbulent cases, the focus is on detailed near-wall phenomenaincluding the viscous sub-layer, buffer layer, and log-law region—as well as the complex interactions among eddies of various scales. Both numerical and quantitative analyses demonstrate that TSA-PINN offers substantial improvements over conventional PINN models. This research advances physics-informed machine learning, setting a new benchmark for modeling dynamic systems in scientific computing and engineering.
翻译:
我们介绍 TSA-PINN,一种新型物理知情神经网络(PINN),利用可训练正弦激活(TSA)机制近似纳维-斯托克斯方程的解。通过结合具有可训练频率的神经元正弦激活功能和动态斜坡恢复机制,TSAPINN 实现了卓越的准确性和收敛性。其动态调节激活频率的能力使复杂流体行为的高效建模成为可能,从而缩短训练时间和计算成本。我们的测试超越了典型问题,还研究了较少被探索且更具挑战性的情景,这些通常对以往模型来说是困难。各种数值测试强调了 TSA-PINN 模型在五种不同情景中的有效性。这些包括在两个不同雷诺数下,盖子驱动腔内的稳态二维流动;一个以振荡流体行为为特征的圆柱尾流问题;以及两个时间相关的三维湍流情况。湍流情况下,重点关注详细的近壁现象,包括粘性亚层、缓冲层和对数定律区域——以及不同尺度涡流之间的复杂相互作用。数值和定量分析均表明,TSA-PINN 相较传统 PINN 模型有显著改进。这项研究推动了基于物理的机器学习,为科学计算和工程中动态系统建模树立了新标杆。
物理信息神经网络(PINN)
PINN 将观测数据和已知的控制方程整合到神经网络模型中,以近似物理系统的解。具体来说,他们估计状态向量 u ^ ( x , t ) \hat{u}(x,t) u ^ ( x , t ) u ( x , t ) u(x,t) u ( x , t ) x ∈ R d x \in \mathbb{R}^d x ∈ R d t ∈ [ 0 , T ] t \in [0,T] t ∈ [ 0 , T ]
系统的控制动力学被非线性算符 N \mathcal{N} N
∂ u ∂ t + N ( u ; x , t ) = 0. (1) \frac{\partial u}{\partial t}+\mathcal{N} \left( u;x,t \right) =0. \tag{1} ∂ t ∂ u + N ( u ; x , t ) = 0. ( 1 ) PINN 模型旨在最小化包含数据忠实度项和物理信息项的损失函数。数据忠实度项旨在最小化预测解与参考解之间的差异
L d a t a = ∑ i = 1 N d a t a ∥ u ^ ( x i , t i ) − u ( x i , t i ) ∥ 2 , (2) L_{\mathrm{data}}=\sum_{i=1}^{{N}_{\mathrm{data}}}{\left\| \hat{{u}}({x}_i,t_i)-{u}({x}_i,t_i) \right\| ^2,}\tag{2} L data = i = 1 ∑ N data ∥ u ^ ( x i , t i ) − u ( x i , t i ) ∥ 2 , ( 2 ) 其中, N d a t a N_{data} N d a t a ( x i , t i ) (x_i,t_i) ( x i , t i )
物理学基础的术语确保预测遵循控制的偏微分方程(PDE),
L p h y s = ∑ j = 1 N p h y s ∥ N ( u ^ ( x j , t j ) ; x j , t j ) ∥ 2 , (3) L_{\mathrm{phys}}=\sum_{j=1}^{{N}_{\mathrm{phys}}}{\left\| \mathcal{N} (\hat{{u}}({x}_j,t_j);{x}_j,t_j) \right\| ^2,}\tag{3} L phys = j = 1 ∑ N phys ∥ N ( u ^ ( x j , t j ) ; x j , t j ) ∥ 2 , ( 3 ) 其中, N p h y s N_{phys} N p h ys
训练的目标是最小化合并损失函数
L P I N N = L d a t a + L p h y s , (4) {L}_{{PINN}}={L}_{{data}}+{L}_{{phys}},\tag{4} L P I NN = L d a t a + L p h ys , ( 4 ) 我们想要的近似解 u ^ ( x , t ) \hat{u}(x,t) u ^ ( x , t ) u ( x , t ) {u}(x,t) u ( x , t )
神经网络
普遍逼近定理证明,即使是带有单一隐藏层的简单多层感知器,也可以通过增加神经元数量,以任意精度近似任意连续函数[43–45]。PINN 模型中广泛使用的架构是前馈神经网络(FFNN),由多个完全连接的层组成。每个神经元在某一层的输出描述为
f i ( x ; w i , b i ) = α ( w i ⋅ x + b i ) , f o r i = 1 , 2 , . . . , n , (5) {f}_i({x};{w}_i,{b}_i)={\alpha }({w}_i\cdot {x}+{b}_i),\quad \mathrm{for}\quad i=1,2,...,n,\tag{5} f i ( x ; w i , b i ) = α ( w i ⋅ x + b i ) , for i = 1 , 2 , ... , n , ( 5 ) 其中, x x x w i w_i w i b i b_i b i i i i α \alpha α
在 Navier-Stokes 方程的近似解中,FFNN 接收空间和时间坐标 X = ( t , x , y , z ) X = (t,x,y,z) X = ( t , x , y , z ) U ( X ) = ( u , v , w ) U(X) = (u, v, w) U ( X ) = ( u , v , w ) P ( X ) P(X) P ( X )
U θ ( X ) , P θ ( X ) = f N N ( X , θ ) , (6) {U\theta }({X}),{P\theta }({X})={f}_{\mathrm{NN}}({X},{\theta }),\tag{6} U θ ( X ) , Pθ ( X ) = f NN ( X , θ ) , ( 6 ) 其中,f N N ( X , θ ) f_{NN} (X,θ) f NN ( X , θ ) θ = w , b θ = w,b θ = w , b θ θ θ
f N N ( x , θ ) = ( a L ∘ α ∘ a L − 1 ∘ ⋯ ∘ α ∘ a 1 ) ( x ) , (7) f_{NN}\left( x,\theta \right) =\left( a_L\circ \alpha \circ a_{L-1}\circ \cdots \circ \alpha \circ a_1 \right) \left( x \right) , \tag{7} f NN ( x , θ ) = ( a L ∘ α ∘ a L − 1 ∘ ⋯ ∘ α ∘ a 1 ) ( x ) , ( 7 ) 其中, a ( x ) = w x + b . a(x) = wx+b. a ( x ) = w x + b .
物理信息神经网络的可训练正弦激活
可训练的正弦激活机制
激活功能的目的是判断神经元应激活还是保持不活跃。在缺乏非线性激活函数的情况下,模型只需利用权重和偏差进行线性变换,这对应于线性回归模型。假设不使用非线性激活函数,这意味着 f ( z ) = z f(z)= z f ( z ) = z
a i = z i = w i a i − 1 + b i , (8) a_i=z_i=w_ia_{i-1}+b_i,\tag{8} a i = z i = w i a i − 1 + b i , ( 8 ) 从输入层开始
a 1 = w 1 x + b 1 , (9) {a}_{{1}}={w}_{{1}}{x}+{b}_{{1}}, \tag{9} a 1 = w 1 x + b 1 , ( 9 ) 第二层
a 2 = w 2 a 2 + b 2 = w 2 ( w 1 x + b 1 ) + b 2 = w 1 w 2 x + w 2 b 1 + b 2 (10) \begin{aligned}
a_2&=w_2a_2+b_2=w_2(w_1x+b_1)+b_2\\
&=w_1w_2x+w_2b_1+b_2\\ \tag{10}
\end{aligned} a 2 = w 2 a 2 + b 2 = w 2 ( w 1 x + b 1 ) + b 2 = w 1 w 2 x + w 2 b 1 + b 2 ( 10 ) 以及第三层
a 3 = w 3 a 2 + b 3 = w 3 ( w 2 w 1 x + w 2 b 1 + b 2 ) + b 3 = w 3 w 2 w 1 x + w 3 w 2 b 1 + w 3 b 2 + b 3 . (11) a_3=w_3a_2+b_3=w_3(w_2w_1x+w_2b_1+b_2)+b_3
\\
\qquad \qquad =w_3w_2w_1x+w_3w_2b_1+w_3b_2+b_3.\tag{11} a 3 = w 3 a 2 + b 3 = w 3 ( w 2 w 1 x + w 2 b 1 + b 2 ) + b 3 = w 3 w 2 w 1 x + w 3 w 2 b 1 + w 3 b 2 + b 3 . ( 11 ) 这一过程持续到到达最后一层 L L L
a L = w L w L − 1 . . . w 2 w 1 x + ( w L w L − 1 . . . w 2 b 1 + w L w L − 1 . . . w 3 b 2 + ⋯ + b L ) . (12) a_L=w_Lw_{L-1}...w_2w_1x+(w_Lw_{L-1}...w_2b_1+w_Lw_{L-1}...w_3b_2+\cdots +b_L).\tag{12} a L = w L w L − 1 ... w 2 w 1 x + ( w L w L − 1 ... w 2 b 1 + w L w L − 1 ... w 3 b 2 + ⋯ + b L ) . ( 12 ) 在最后一层,网络输出可以写成
y = w t o t a l x + b t o t a l (13) {y}={w}_{\mathrm{total}}{x}+{b}_{\mathrm{total}}\tag{13} y = w total x + b total ( 13 ) 其中,w t o t a l = w L w L − 1 . . . w 2 w 1 w_{total} = w_Lw_{L−1}...w_2w_1 w t o t a l = w L w L − 1 ... w 2 w 1 b t o t a l = ( w L w L − 1 . . . w 2 b 1 + w L w L − 1 . . . w 3 b 2 + ⋯ + b L ) b_{total} = (w_Lw_{L−1} ...w_2b_1 + w_Lw_{L−1} ...w_3b_2 + ⋯ + b_L) b t o t a l = ( w L w L − 1 ... w 2 b 1 + w L w L − 1 ... w 3 b 2 + ⋯ + b L ) x x x k k k i i i
z i ( k ) = w i ( k ) ⋅ a ( k − 1 ) + b i ( k ) , (14) {z}_{{i}}^{{(k)}}=\mathbf{w}_{i}^{(k)}\cdot \mathbf{a}^{(k-1)}+b_{i}^{(k)},\tag{14} z i ( k ) = w i ( k ) ⋅ a ( k − 1 ) + b i ( k ) , ( 14 ) 其中,a ( k − 1 ) ∈ R n k − 1 \mathbf{a}^{\left( k-1 \right)}\in \mathbb{R} ^{n_{k-1}} a ( k − 1 ) ∈ R n k − 1 k − 1 k-1 k − 1 w i ( k ) ∈ R n k − 1 \mathbf{w}_{i}^{(k)}\in \mathbb{R} ^{n_{k-1}} w i ( k ) ∈ R n k − 1 K K K i i i b i ( k ) ∈ R b_{i}^{\left( k \right)}\in R b i ( k ) ∈ R i i i z i ( k ) ∈ R z_{i}^{\left( k \right)}\in R z i ( k ) ∈ R
在本研究中,我们使用一个按神经元划分的正弦激活函数,其频率为可训练的 f i ( k ) ∈ R f_{i}^{\left( k \right)}\in \mathbb{R} f i ( k ) ∈ R
ψ i ( k ) = sin ( f i ( k ) z i ( k ) ) , (15) \psi _{i}^{\left( k \right)}=\sin \left( f_{i}^{\left( k \right)}z_{i}^{\left( k \right)} \right) , \tag{15} ψ i ( k ) = sin ( f i ( k ) z i ( k ) ) , ( 15 ) ϕ i ( k ) = cos ( f i ( k ) z i ( k ) ) , (16) \phi _{i}^{\left( k \right)}=\cos \left( f_{i}^{\left( k \right)}z_{i}^{\left( k \right)} \right) , \tag{16} ϕ i ( k ) = cos ( f i ( k ) z i ( k ) ) , ( 16 ) a i ( k ) = ζ 1 ψ i ( k ) + ζ 2 ϕ i ( k ) = ζ 1 sin ( f i ( k ) z i ( k ) ) + ζ 2 cos ( f i ( k ) z i ( k ) ) , (17) a_{i}^{(k)}=\zeta _1\psi _{i}^{(k)}+\zeta _2\phi _{i}^{(k)}=\zeta _1\sin\mathrm{(}f_{i}^{(k)}z_{i}^{(k)})+\zeta _2\cos\mathrm{(}f_{i}^{(k)}z_{i}^{(k)}),\tag{17} a i ( k ) = ζ 1 ψ i ( k ) + ζ 2 ϕ i ( k ) = ζ 1 sin ( f i ( k ) z i ( k ) ) + ζ 2 cos ( f i ( k ) z i ( k ) ) , ( 17 ) 其中,ζ 1 , ζ 2 ∈ R \zeta_1,\zeta_2\in \mathbb{R} ζ 1 , ζ 2 ∈ R
设 a ( k − 1 ) ∈ R n k − 1 a(k−1)\in \mathbb{R}^{n_{k−1}} a ( k − 1 ) ∈ R n k − 1 k k k
z ( k ) = W ( k ) a ( k − 1 ) + b ( k ) , (18) \mathbf{z}^{(k)}=\mathbf{W}^{(k)}\mathbf{a}^{(k-1)}+\mathbf{b}^{(k)}, \tag{18} z ( k ) = W ( k ) a ( k − 1 ) + b ( k ) , ( 18 ) 其中,W ( k ) ∈ R n k × n k − 1 \mathbf{W}^{(k)}\in \mathbb{R} ^{n_k\times n_{k-1}} W ( k ) ∈ R n k × n k − 1 k k k b ( k ) ∈ R n k b^{\left( k \right)}\in R^{n_k} b ( k ) ∈ R n k z ( k ) ∈ R n k z^{\left( k \right)}\in R^{n_k} z ( k ) ∈ R n k
元素间正弦激活使用可训练频率向量 f ( k ) ∈ R n k f^{\left( k \right)}\in R^{n_k} f ( k ) ∈ R n k
ψ ( k ) = sin ( f ( k ) ⊙ z ( k ) ) , (19) \psi ^{\left( k \right)}=\sin \left( f^{\left( k \right)}\odot z^{\left( k \right)} \right) ,\tag{19} ψ ( k ) = sin ( f ( k ) ⊙ z ( k ) ) , ( 19 ) ϕ ( k ) = cos ( f ( k ) ⊙ z ( k ) ) , (20) \phi ^{\left( k \right)}=\cos \left( f^{\left( k \right)}\odot z^{\left( k \right)} \right) ,\tag{20} ϕ ( k ) = cos ( f ( k ) ⊙ z ( k ) ) , ( 20 ) 其中,⊙ \odot ⊙
当 N = n k N = n_k N = n k k k k
a ( k ) = [ a 1 ( k ) a 2 ( k ) ⋮ a N ( k ) ] = [ ζ 1 sin ( f 1 ( k ) z 1 ( k ) ) + ζ 2 cos ( f 1 ( k ) z 1 ( k ) ) ζ 1 sin ( f 2 ( k ) z 2 ( k ) ) + ζ 2 cos ( f 2 ( k ) z 2 ( k ) ) ⋮ ζ 1 sin ( f N ( k ) z N ( k ) ) + ζ 2 cos ( f N ( k ) z N ( k ) ) ] . (21) \mathbf{a}^{(k)}=\left[ \begin{array}{c}
a_{1}^{(k)}\\
a_{2}^{(k)}\\
\vdots\\
a_{N}^{(k)}\\
\end{array} \right] =\left[ \begin{array}{c}
\zeta _1\sin\mathrm{(}f_{1}^{(k)}z_{1}^{(k)})+\zeta _2\cos\mathrm{(}f_{1}^{(k)}z_{1}^{(k)})\\
\zeta _1\sin\mathrm{(}f_{2}^{(k)}z_{2}^{(k)})+\zeta _2\cos\mathrm{(}f_{2}^{(k)}z_{2}^{(k)})\\
\vdots\\
\zeta _1\sin\mathrm{(}f_{N}^{(k)}z_{N}^{(k)})+\zeta _2\cos\mathrm{(}f_{N}^{(k)}z_{N}^{(k)})\\
\end{array} \right] .\tag{21} a ( k ) = a 1 ( k ) a 2 ( k ) ⋮ a N ( k ) = ζ 1 sin ( f 1 ( k ) z 1 ( k ) ) + ζ 2 cos ( f 1 ( k ) z 1 ( k ) ) ζ 1 sin ( f 2 ( k ) z 2 ( k ) ) + ζ 2 cos ( f 2 ( k ) z 2 ( k ) ) ⋮ ζ 1 sin ( f N ( k ) z N ( k ) ) + ζ 2 cos ( f N ( k ) z N ( k ) ) . ( 21 ) 这种表述使每个神经元能够独立适应其激活频率,使网络能够在不同神经元之间表示具有不同且可能高频成分的功能。
Slope recovery
边坡恢复项 S ( a ) S(a) S ( a )
S ( a ) = 1 1 L − 1 ∑ k = 1 L − 1 exp ( 1 N k ∑ i = 1 N k f i k ) , (22) S\left( a \right) =\frac{1}{\frac{1}{L-1}\sum_{k=1}^{L-1}{\exp \left( \frac{1}{N_k}\sum_{i=1}^{N_k}{f_{i}^{k}} \right)}},\tag{22} S ( a ) = L − 1 1 ∑ k = 1 L − 1 exp ( N k 1 ∑ i = 1 N k f i k ) 1 , ( 22 ) 其中,L L L N k N_k N k f i k {f}_{{i}}^{{k}} f i k k k k i i i
斜率恢复项被包含在损失函数中,以调节可训练频率对训练动力学的影响。带边坡恢复项的增减损函数写作
L P I N N = L d a t a + L p h y s + λ S ( a ) , (23) L_{PINN}=L_{data}+L_{phys}+\lambda S\left( a \right) ,\tag{23} L P I NN = L d a t a + L p h ys + λ S ( a ) , ( 23 ) 其中, λ λ λ
损失函数
为了建立与 TSA-PINN 模型相关的损耗函数,考虑了一个涉及三维时间依赖湍流通道流的问题。控制流动的不可压缩纳维-斯托克斯方程以速度-压力(VP)形式表示:
∂ u ∂ t + u ⋅ ∇ u + ∇ p − 1 R e Δ u = 0 , i n Ω ; (24) \frac{\partial {u}}{\partial t}+{u}\cdot \nabla {u}+\nabla p-\frac{1}{Re}\Delta {u}=0,\hskip 28.4528pt \mathrm{in}\hskip 5.69055pt \Omega ; \tag{24} ∂ t ∂ u + u ⋅ ∇ u + ∇ p − R e 1 Δ u = 0 , in Ω ; ( 24 ) ∇ ⋅ u = 0 , i n Ω ; (25) \nabla \cdot {u}=0,\qquad \qquad \qquad \qquad \qquad \qquad \mathrm{in}\Omega ; \tag{25} ∇ ⋅ u = 0 , in Ω ; ( 25 ) u = u Γ , o n Γ D ; (26) {u}={u}_{\Gamma},\qquad \qquad \qquad \qquad \qquad \qquad \quad on\,\, \Gamma _D; \tag{26} u = u Γ , o n Γ D ; ( 26 ) ∂ u ∂ n = 0 , o n Γ N . (27) \frac{\partial {u}}{\partial n}=0,\qquad \qquad \qquad \qquad \qquad \qquad on\Gamma _{{N}}.\tag{27} ∂ n ∂ u = 0 , o n Γ N . ( 27 ) 在此内容中,无维时间为 t t t u ( x , y , z , t ) = [ u , v , w ] T u(x,y,z,t) = [u,v,w]^T u ( x , y , z , t ) = [ u , v , w ] T P P P R e Re R e R e = ρ u L μ Re=\frac{\rho uL}{\mu} R e = μ ρ uL ρ ρ ρ u u u L L L μ μ μ
R x = ∂ t u + u ∂ x u + υ ∂ y u + υ υ ∂ Z u + ∂ X p − 1 R e ( ∂ x x 2 u + ∂ y y 2 u + ∂ Z z 2 u ) ; (28) R_x=\partial _tu+u\partial _{_x}u+\upsilon \partial _{_y}u+\upsilon \upsilon \partial _{_Z}u+\partial _{_X}p -\frac{1}{Re}(\partial _{xx}^{2}u+\partial _{yy}^{2}u+\partial _{_Zz}^{2}u);\tag{28} R x = ∂ t u + u ∂ x u + υ ∂ y u + υυ ∂ Z u + ∂ X p − R e 1 ( ∂ xx 2 u + ∂ yy 2 u + ∂ Z z 2 u ) ; ( 28 ) R y = ∂ t υ + u ∂ x υ + υ ∂ y υ + υ ∂ z υ + ∂ y p − 1 R e ( ∂ x x 2 υ + ∂ y y 2 υ + ∂ z z 2 υ ) ; (29) R_y=\partial _t\upsilon +u\partial _x\upsilon +\upsilon \partial _y\upsilon +\upsilon \partial _z\upsilon +\partial _yp-\frac{1}{Re}(\partial _{xx}^{2}\upsilon +\partial _{yy}^{2}\upsilon +\partial _{zz}^{2}\upsilon );\tag{29} R y = ∂ t υ + u ∂ x υ + υ ∂ y υ + υ ∂ z υ + ∂ y p − R e 1 ( ∂ xx 2 υ + ∂ yy 2 υ + ∂ zz 2 υ ) ; ( 29 ) R z = ∂ t w + u ∂ x w + υ ∂ y w + w ∂ z w + ∂ z p − 1 R e ( ∂ x x 2 w + ∂ y y 2 w + ∂ z z 2 w ) ; (30) {R}_z=\partial _t{w}+{u}\partial _x{w}+{\upsilon }\partial _y{w}+{w}\partial _z{w}+\partial _z{p}-\frac{1}{{Re}}(\partial _{xx}^{2}{w}+\partial _{yy}^{2}{w}+\partial _{zz}^{2}{w});\tag{30} R z = ∂ t w + u ∂ x w + υ ∂ y w + w ∂ z w + ∂ z p − R e 1 ( ∂ xx 2 w + ∂ yy 2 w + ∂ zz 2 w ) ; ( 30 ) R c = ∂ x u + ∂ y v + ∂ z w . (31) R_c=\partial _xu+\partial _yv+\partial _zw.\tag{31} R c = ∂ x u + ∂ y v + ∂ z w . ( 31 ) 这里,R x R_x R x R y R_y R y R z R_z R z R c R_c R c x x x y y y z z z x x x y y y z z z t t t w w w b b b f f f
L = L I C + L B C + L R + λ L S , (32) {L}={L}_{{IC}}+{L}_{{BC}}+{L}_{{R}}+\lambda {L}_{{S}},\tag{32} L = L I C + L BC + L R + λ L S , ( 32 ) 以及损失函数项可以写成:
L I C = 1 N 1 ∑ n = 1 N 1 ∣ u θ n − u I C n ∣ 2 ; (33) L_{IC}=\frac{1}{N_1}\sum_{n=1}^{N_1}{\bigl| u_{\theta}^{n}-u_{IC}^{n} \bigr| ^2;}\tag{33} L I C = N 1 1 n = 1 ∑ N 1 u θ n − u I C n 2 ; ( 33 ) L B C = 1 N B ∑ n = 1 N B ∣ u θ n − u B C n ∣ 2 ; (34) {L}_{{BC}}=\frac{1}{{N}_{{B}}}\sum_{{n}={1}}^{{N}_{{B}}}{\left| u_{\theta}^{n}-u_{\mathrm{BC}}^{n} \right|^2};\tag{34} L BC = N B 1 n = 1 ∑ N B ∣ u θ n − u BC n ∣ 2 ; ( 34 ) L R = 1 N R ( ∑ n = 1 N R ∣ R x n ∣ 2 + ∑ n = 1 N R ∣ R y n ∣ 2 + ∑ n = 1 N R ∣ R z n ∣ 2 + ∑ n = 1 N R ∣ R c n ∣ 2 ) , (35) L_{\mathrm{R}}=\frac{1}{N_{\mathrm{R}}}\biggl( \sum_{n=1}^{N_{\mathrm{R}}}{\bigl| R_{x}^{n} \bigr| ^2}+\sum_{n=1}^{N_{\mathrm{R}}}{\bigl| R_{y}^{n} \bigr| ^2}+\sum_{n=1}^{N_{\mathrm{R}}}{\bigl| R_{z}^{n} \bigr| ^2}+\sum_{n=1}^{N_{\mathrm{R}}}{\bigl| R_{c}^{n} \bigr| ^2} \biggr) ,\tag{35} L R = N R 1 ( n = 1 ∑ N R R x n 2 + n = 1 ∑ N R R y n 2 + n = 1 ∑ N R R z n 2 + n = 1 ∑ N R R c n 2 ) , ( 35 ) 其中,L I C L_{IC} L I C L B C L_{BC} L BC L R L_R L R I C IC I C B C BC BC
W ∗ = a r g min w ( L ( w ) ) ; (36) W^*=arg\min_w \left( L\left( w \right) \right) ;\tag{36} W ∗ = a r g w min ( L ( w ) ) ; ( 36 ) b ∗ = a r g min b ( L ( b ) ) ; (37) b^*=arg\min_b \left( L\left( b \right) \right) ;\tag{37} b ∗ = a r g b min ( L ( b ) ) ; ( 37 ) f ∗ = a r g min f ( L ( f ) ) . (38) f^*=arg\min_f \left( L\left( f \right) \right) .\tag{38} f ∗ = a r g f min ( L ( f ) ) . ( 38 ) 该最小化问题通过梯度下降方法近似。模型参数更新如下:
w m + 1 = w m − η ∇ w m L m ( w ) ; (39) {w}^{{m}+{1}}={w}^{{m}}-\eta \nabla _{{w}^{{m}}}{L}^{{m}}({w});\tag{39} w m + 1 = w m − η ∇ w m L m ( w ) ; ( 39 ) b m + 1 = b m − η ∇ b m L m ( b ) ; (40) {b}^{{m}+{1}}={b}^{{m}}-{\eta }\nabla _{{b}^{{m}}}{L}^{{m}}{(b)};\tag{40} b m + 1 = b m − η ∇ b m L m ( b ) ; ( 40 ) f m + 1 = f m − η ∇ f m L m ( f ) , (41) f^{m+1}=f^m-\eta \nabla _{f^m}L^m(f),\tag{41} f m + 1 = f m − η ∇ f m L m ( f ) , ( 41 ) 其中,在第 m m m η η η L m L_m L m
结果与讨论
这里边提出了五个算例,三个二维算例,两个三维算例。
为了验证 TSA-PINN 的特性,应用它在各种场景下近似纳维斯托克斯方程:
Re = 100 时的二维稳态盖驱动腔问题;
Re = 3200 处的二维稳态盖驱动腔问题;
二维时变圆柱尾迹;
3D 时间依赖湍流通道流:近壁区;
3D 时间依赖湍流通道流动:覆盖更大范围。
为了估计每种情景相关的误差,使用所有评估点误差的相对 L 2 L_2 L 2
E r r o r i = ∥ U ^ i − U i ∥ 2 ∥ U i ∥ 2 × 100 , (42) \mathrm{Error}_i=\frac{\left\| \hat{{U}}_i-{U}_i \right\| _2}{\left\| {U}_i \right\| _2}\times 100, \tag{42} Error i = ∥ U i ∥ 2 U ^ i − U i 2 × 100 , ( 42 ) 其中,下标 i i i ‖ ⋅ ‖ 2 ‖⋅‖_2 ‖ ⋅ ‖ 2 L 2 L_2 L 2 U ^ \hat{U} U ^ U U U σ = 1.0 \sigma = 1.0 σ = 1.0
Re = 100 时的二维稳态盖驱动腔问题;
第一个测试用例是在二维盖驱动腔内的稳态流动,受二维稳态不可压缩纳维斯托克斯方程(24)和(25)控制。对于这个问题,我们将雷诺数设为 R e = 100 Re = 100 R e = 100 x ∈ [ 0 , 1 ] x \in [0, 1] x ∈ [ 0 , 1 ] y ∈ [ 0 , 1 ] y \in [0, 1] y ∈ [ 0 , 1 ] ψ ψ ψ P P P
u x + v y = 0. (43) u_x+v_y=0.\tag{43} u x + v y = 0. ( 43 ) 在此环境中,速度分量为
u = ∂ y ψ , (44) u=\partial _y\psi ,\tag{44} u = ∂ y ψ , ( 44 ) 以及
\upsilon =-\partial _x\psi .\tag{45}
该假设自动满足连续性约束。需要注意的是,该领域内没有针对该问题的训练数据。培训完全依赖于无监督学习,使用领域内 4000 个搭配点,以及沿边界的 500 个边界条件点。在此情境下,控制方程的残差为:
R x = u ∂ x u + υ ∂ y u + ∂ x p − 1 R e ( ∂ x x 2 u + ∂ y y 2 u ) ; (46) R_x=u\partial _xu+\upsilon \partial _yu+\partial _xp-\frac{1}{Re}(\partial _{xx}^{2}u+\partial _{yy}^{2}u);\tag{46} R x = u ∂ x u + υ ∂ y u + ∂ x p − R e 1 ( ∂ xx 2 u + ∂ yy 2 u ) ; ( 46 ) R y = u ∂ x υ + υ ∂ y υ + ∂ y p − 1 R e ( ∂ x x 2 υ + ∂ y y 2 υ ) . (47) R_y=u\partial _x\upsilon +\upsilon \partial _y\upsilon +\partial _yp-\frac{1}{Re}(\partial _{xx}^{2}\upsilon +\partial _{yy}^{2}\upsilon ).\tag{47} R y = u ∂ x υ + υ ∂ y υ + ∂ y p − R e 1 ( ∂ xx 2 υ + ∂ yy 2 υ ) . ( 47 ) 这些项被包含在损失函数中,以满足物理知情部分。学习率设定为指数衰减,起始于初始值 η = 10 − 3 η = 10^{-3} η = 1 0 − 3 1000 1000 1000 0.9 0.9 0.9 8000 8000 8000 400 × 400 400×400 400 × 400 5 5 5 50 50 50
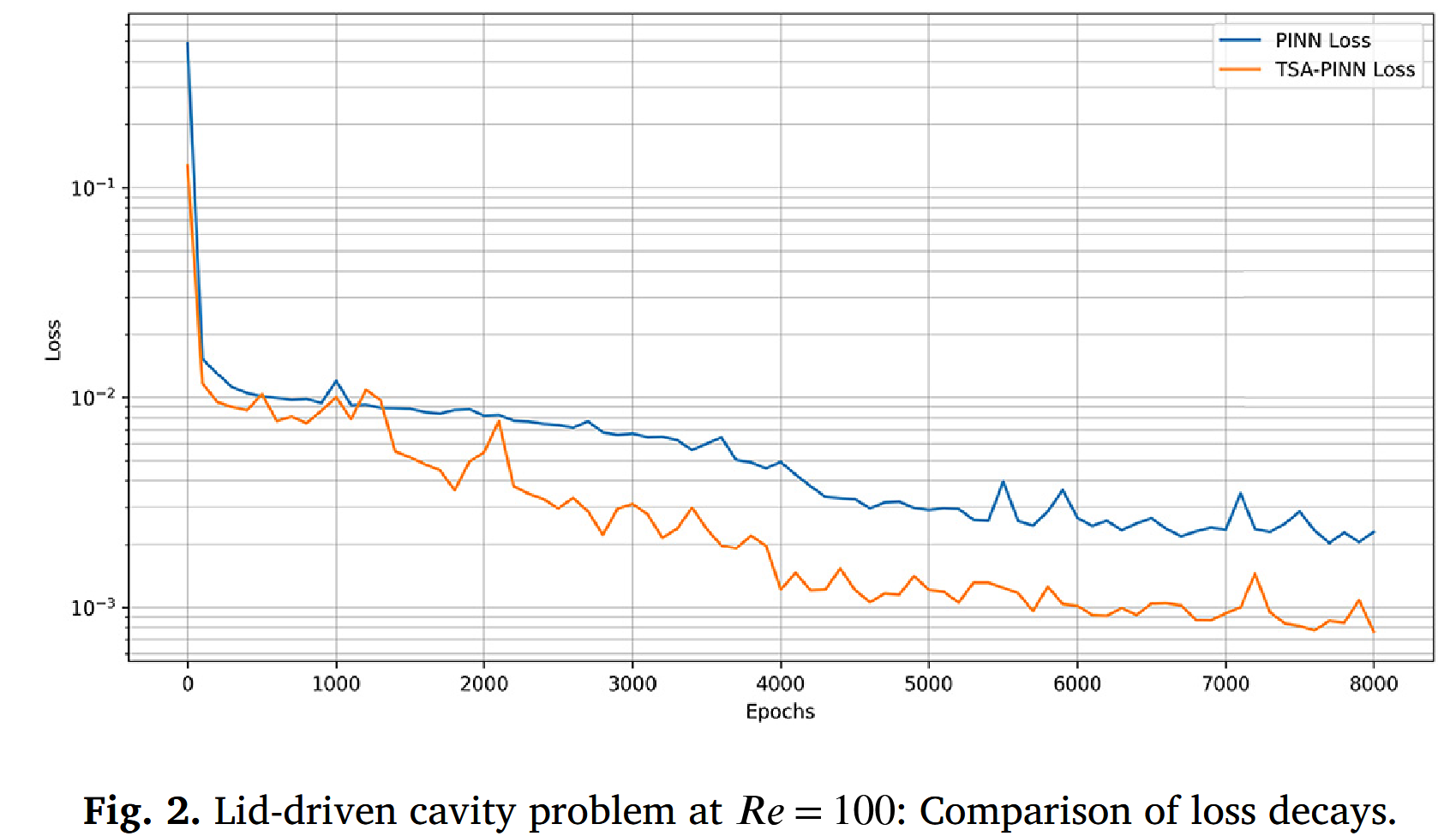
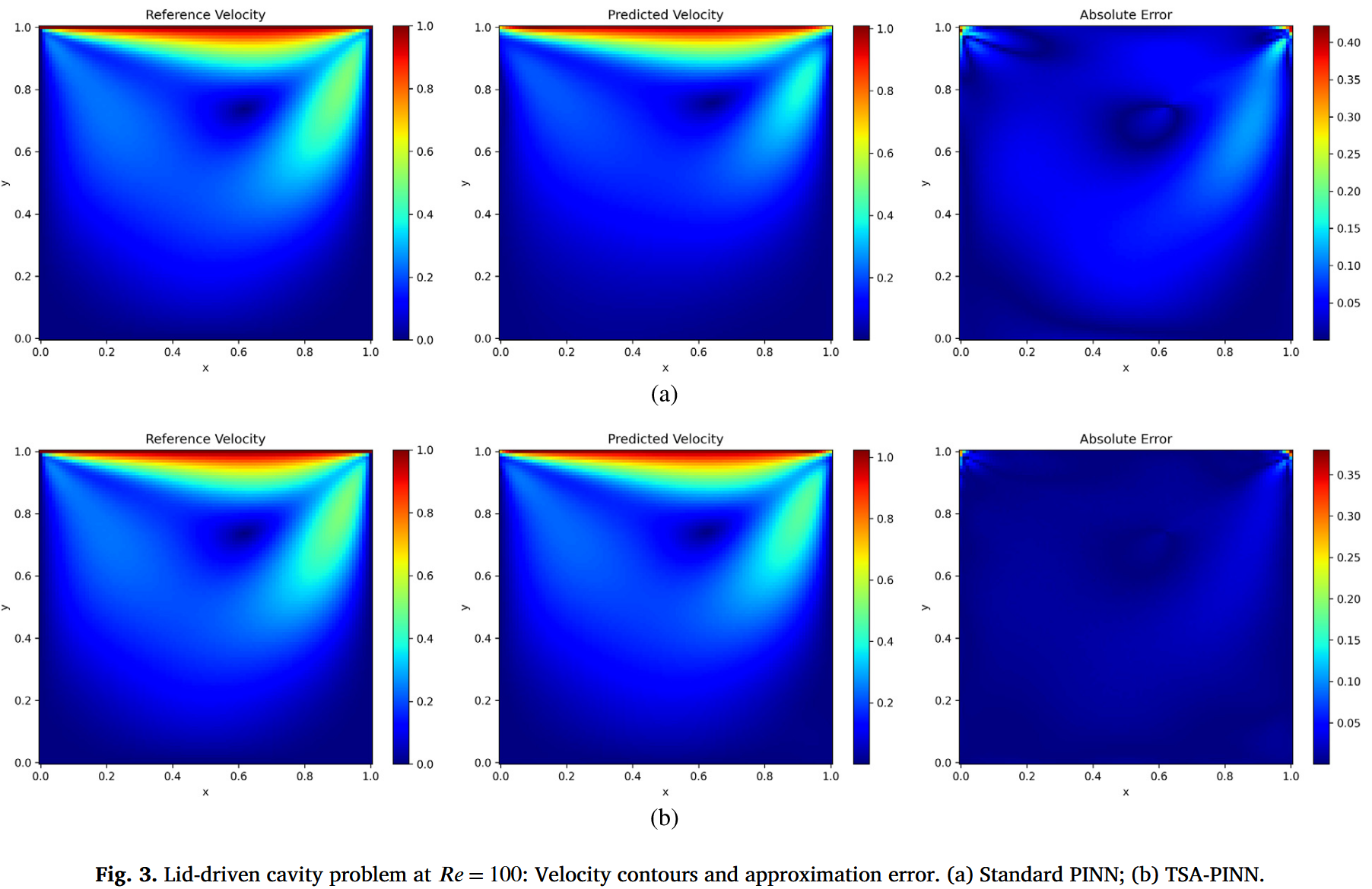
与标准 PINN 相比,TSA-PINN 的一个主要优势是其增强的模型表达性,这得益于采用可训练频率的神经元级正弦激活函数,从而实现更快的收敛速度。图 2 显示,TSA-PINN 的损耗衰减速度显著快于标准 PINNs,快近半个数量级。这一改进在图 3 中得到了进一步说明。虽然使用标准 PINN 的模拟难以准确捕捉速度场(图 3-a),但 TSAPINN 误差极小,准确捕捉所有现象(图 3-b)。
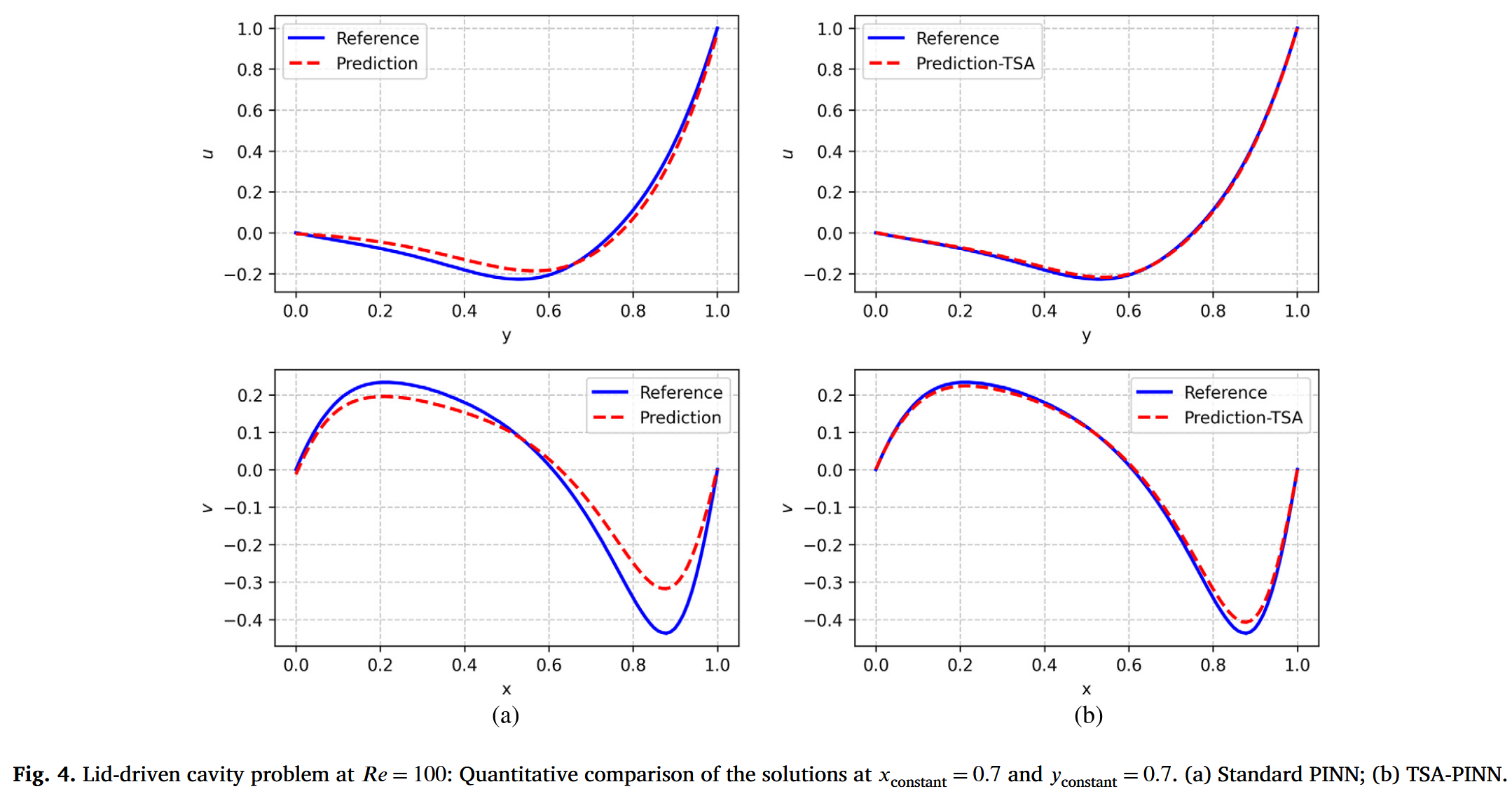
图 4 展示了 TSA-PINN(图 4-b)和标准 PINN(图 4-a)所做近似的定量分析。该分析定量地重申了先前结论,凸显了 TSA-PINN 的卓越准确性。TSA-PINN 所做的近似几乎与参考解完全一致。标�准 PINN 近似显示明显误差。表 1 比较了 TSA-PINN 与标准 PINN 之间 L2 范数近似误差的差异。TSA-PINN 的准确度高于标准 PINN,后者的误差减少了一个数量级。这种准确度的提升代价是大约增加了 24 % 24\% 24%
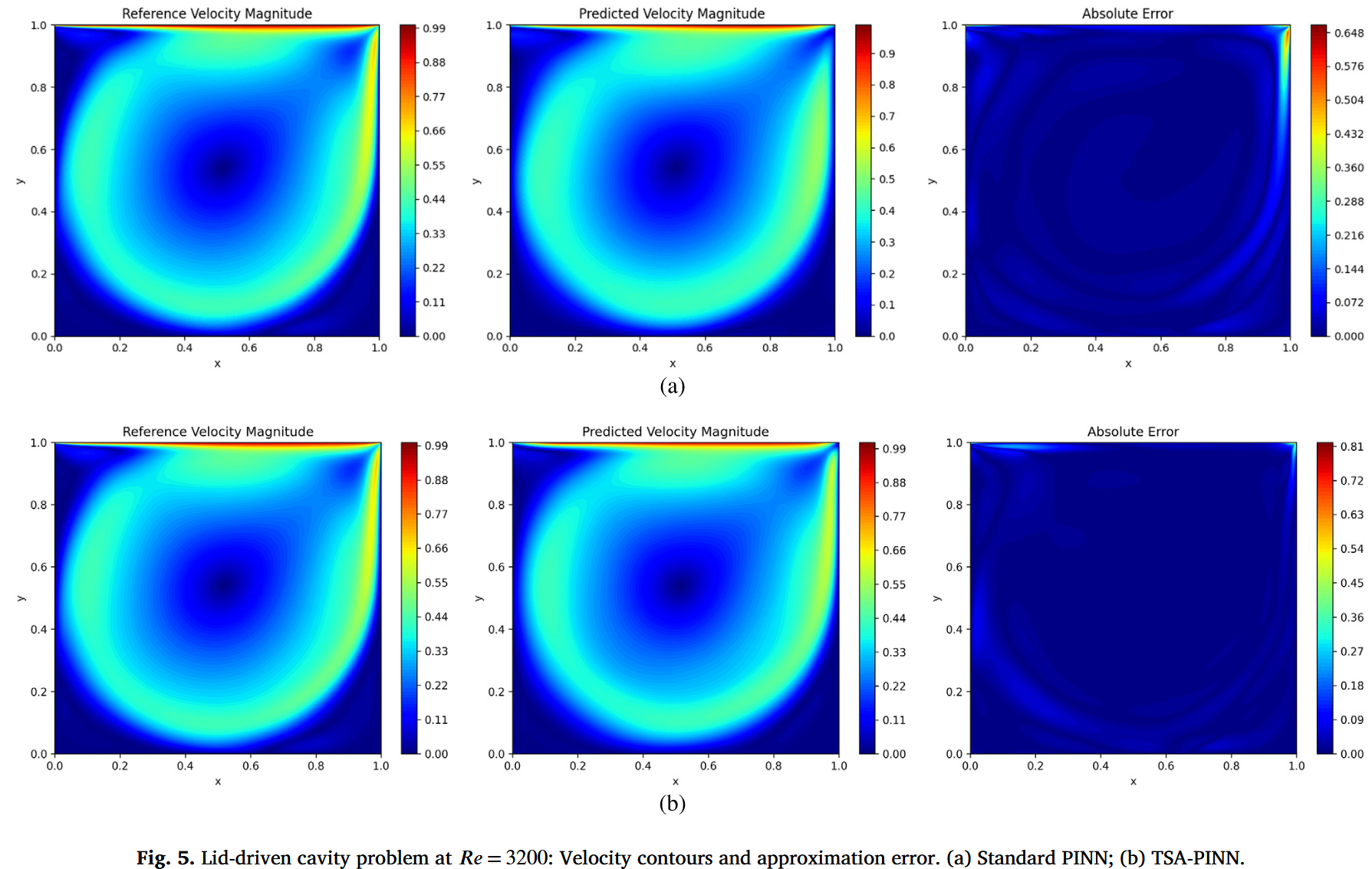
Re = 3200 处的二维盖子驱动腔问题
为了进一步评估 TSA-PINN 在处理更具挑战性流动问题中的鲁棒性和能力,我们将该方法应用于由不可压缩纳维-斯托克斯方程控制的二维盖子驱动腔问题,雷诺数为 R e y o l d s Reyolds R eyo l d s R e = 3200 Re = 3200 R e = 3200
u ( x , y ) = 1 − cosh ( C 0 ( x − 0.5 ) ) cosh ( 0.5 C 0 ) , (48) u\left( x,y \right) =1-\frac{\cosh \left( C_0\left( x-0.5 \right) \right)}{\cosh \left( 0.5C_0 \right)},\tag{48} u ( x , y ) = 1 − cosh ( 0.5 C 0 ) cosh ( C 0 ( x − 0.5 ) ) , ( 48 ) υ ( x , y ) = 0 , (49) \upsilon \left( x,y \right) =0,\tag{49} υ ( x , y ) = 0 , ( 49 ) 其中,x ∈ [ 0 , 1 ] , y = 1 , C 0 = 50 x \in [0,1],y=1,C_0=50 x ∈ [ 0 , 1 ] , y = 1 , C 0 = 50 7000 7000 7000 1000 1000 1000 1000 1000 1000
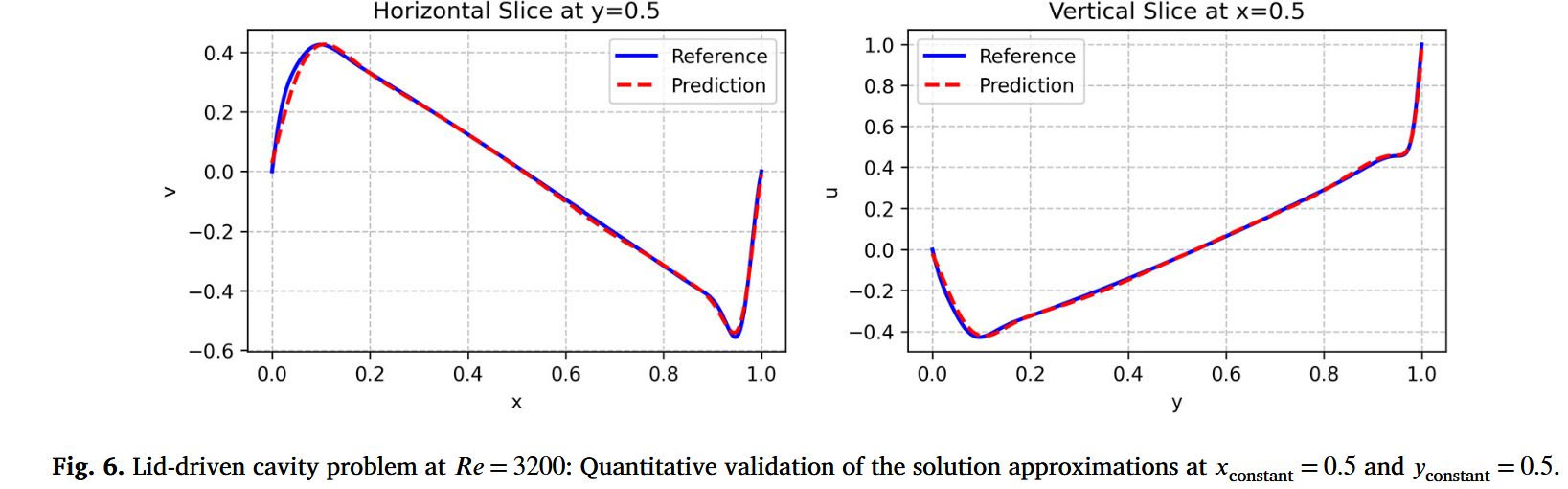
对于 R e = 3200 Re = 3200 R e = 3200
图 7 显示了两种方法的损失历史。TSA-PINN 表现出更平滑、更稳定的收敛行为,最终损失值低于标准 PINN,这表明训练效率和数值稳定性有所提升。最后,表 2 总结了标准 PINN 与 TSA-PINN 之间的错误度量和运行时间比较。尽管 TSA-PINN 的训练时间略有增加,但其显著的近似误差降低使其成为模拟 Re = 3200 处复杂流动现象的更稳健高效选择。
二维时变圆柱尾迹
第二个问题是对 Re = 100 时圆柱体后方二维涡旋脱落的时间依赖模拟。该问题由二维不可压缩纳维–斯托克斯方程(24)和(25)所支配。 入口条件指定为自由流无量纲速度 u ∞ = 1 u_{\infty} = 1 u ∞ = 1 ν = 0.01 ν = 0.01 ν = 0.01 D = 1 D = 1 D = 1 ( x , y ) = ( 0 , 0 ) (x,y) = (0,0) ( x , y ) = ( 0 , 0 ) [ 1 , 8 ] × [ − 2 , 2 ] [1,8] ×[−2,2] [ 1 , 8 ] × [ − 2 , 2 ] [ 0 , 20 ] [0,20] [ 0 , 20 ] Δ t = 0.01 \Delta t = 0.01 Δ t = 0.01 x x x y y y t t t ψ ( x , y , t ) ψ(x,y,t) ψ ( x , y , t ) p ( x , y , t ) p(x,y,t) p ( x , y , t ) 200 200 200 1000 1000 1000 400 400 400 4 4 4 50 50 50 η = 5 × 10 − 3 η = 5 × 10^{-3} η = 5 × 1 0 − 3 1000 1000 1000 0.95 0.95 0.95 4000 4000 4000 L 2 L^2 L 2 200 × 200 200×200 200 × 200
R x = ∂ t u + u ∂ x u + υ ∂ y u + ∂ x p − 1 R e ( ∂ x x 2 u + ∂ y y 2 u ) ; R y = ∂ t υ + u ∂ x υ + υ ∂ y υ + ∂ y p − 1 R e ( ∂ x x 2 υ + ∂ y y 2 υ ) . (50,51) \begin{aligned}
R_x&=\partial _tu+u\partial _xu+\upsilon \partial _yu+\partial _xp-\frac{1}{Re}(\partial _{xx}^{2}u+\partial _{yy}^{2}u);\tag{50,51} \\
R_y&=\partial _t\upsilon +u\partial _x\upsilon +\upsilon \partial _y\upsilon +\partial _yp-\frac{1}{Re}(\partial _{xx}^{2}\upsilon +\partial _{yy}^{2}\upsilon ).\\
\end{aligned} R x R y = ∂ t u + u ∂ x u + υ ∂ y u + ∂ x p − R e 1 ( ∂ xx 2 u + ∂ yy 2 u ) ; = ∂ t υ + u ∂ x υ + υ ∂ y υ + ∂ y p − R e 1 ( ∂ xx 2 υ + ∂ yy 2 υ ) . ( 50,51 ) 首先,我们分析 TSA-PINN 模型中可训练频率初始化的作用。尽管 TSA-PINN 内部频率具有适应性,初始化仍会影响优化。频率的初始值更适合与目标函数的谱特性对齐,使优化器更高效地收敛至最优参数值。图 8 展示了标准 PINN 与初始化为不同频率值 σ \sigma σ σ = 1.0 \sigma = 1.0 σ = 1.0 σ = 1.0 \sigma = 1.0 σ = 1.0 σ = 3.0 \sigma = 3.0 σ = 3.0 σ = 1.0 \sigma = 1.0 σ = 1.0 σ = 0.1 \sigma =0.1 σ = 0.1 σ = 3.0 \sigma = 3.0 σ = 3.0
图 9 展示了 TSA-PINN 模型在 σ \sigma σ σ = 1.0 \sigma = 1.0 σ = 1.0 σ \sigma σ σ \sigma σ σ \sigma σ
图 10 展示了 t = 10.0 t = 10.0 t = 10.0
图 11 展示了圆柱尾流中固定点速度分量的时间演变,提供了 TSA-PINN 与标准 PINN 模型与参考数据的定量比较。此次比较验证了模型,展示了它们捕捉流体动力学随时间变化的能力。TSA-PINN 模型与参考数据高度一致,在极快且短的训练过程中准确复现了两个速度分量的正弦振荡(见表 3)。这种对流动振荡幅度和相位的精确捕捉,凸显了 TSA-PINN 可训练正弦激活函数的有效性,这些函数更适合此类流体动力学问题,其中底层解表现出正弦行为。相比之下,标准 PINN 无法准确匹配参考解。此次比较的定量结果不仅验证了 TSAPINN 模型,也强调了其在准确性和稳健性的优势。TSA-PINN 的性能提升显示其动态调节激活频率的能力。表 3 详细比较了标准 PINN 与 TSA-PINN 之间的 L 2 L^2 L 2 L 2 L^2 L 2 u u u L 2 L^2 L 2 1.96 × 10 − 2 1.96 × 10^{-2} 1.96 × 1 0 − 2 6.41 × 10 − 1 6.41 × 10^{-1} 6.41 × 1 0 − 1 6.63 × 10 − 1 6.63 × 10^{-1} 6.63 × 1 0 − 1 6.78 × 10 − 1 6.78 × 10^{-1} 6.78 × 1 0 − 1
三维时间相关湍流通道流动:近壁区域
在第三个测试和验证场景中,我们将模型应用于更复杂且更现实的挑战,对 R e = 999.4 Re = 999.4 R e = 999.4 ( 24 ) (24) ( 24 ) ( 25 ) (25) ( 25 ) https://turbulence.pha.jhu.edu/ 。
模拟的空间域分别为 [ 0 , 8 π ] × [ − 1 , 1 ] × [ 0 , 3 π ] [0,8 \pi] × [−1,1] × [0,3 \pi] [ 0 , 8 π ] × [ − 1 , 1 ] × [ 0 , 3 π ] x x x y y y z z z 0.0065 0.0065 0.0065 ν = 5 × 10 ⁻ 5 ν = 5 × 10^{⁻5} ν = 5 × 1 0 ⁻5 ( x , y , z , t ) (x,y,z,t) ( x , y , z , t ) ( u , v , w , P ) (u,v,w,P) ( u , v , w , P ) x x x y y y z z z [ 12.47 , 12.66 ] × [ − 1.00 , − 0.90 ] × [ 4.69 , 4.75 ] [12.47,12.66] ×[−1.00,−0.90] ×[4.69,4.75] [ 12.47 , 12.66 ] × [ − 1.00 , − 0.90 ] × [ 4.69 , 4.75 ]
粘性亚层,或称层流亚层,位于壁面附近,流动主要为粘性,湍流最小。在该区域,速度轮廓几乎是线性的,剪切应力主要为粘性。粘性效应占主导,速度梯度与剪切应力成正比,使该层相较其他层非常薄。
缓冲层位于粘性亚层之上、完全湍流区之下,作为粘性和湍流效应交织的过渡区。该层对粘性剪切和湍流剪切都具有重要意义,其特征是复杂的速度分布,既不遵循简单的线性定理也不遵循对数定律。它标志着湍流产生和耗散大致平衡的区域。
位于缓冲层上方的对数定律区域由完全湍流控制,与湍流的惯性效应相比,粘性效应可忽略不计。该区域内的平均速度分布随距离墙壁的对数分布,
u + = 1 k log ( y + ) + B , (52) u^+=\frac{1}{k}\log \left( y^+ \right) +B,\tag{52} u + = k 1 log ( y + ) + B , ( 52 ) 其中, u + u^+ u + y + y^+ y + k k k 0.41 0.41 0.41 B B B 5.2 5.2 5.2
在该模拟中,每个时间步计算模型的损失,使用 10 , 000 10,000 10 , 000 6 , 644 6,644 6 , 644 10 , 000 10,000 10 , 000 8 8 8 200 200 200 150 150 150 10 − 3 10^{-3} 1 0 − 3 200 200 200 10 − 4 10^{-4} 1 0 − 4 200 200 200 5 × 10 − 5 5×10^{-5} 5 × 1 0 − 5 250 250 250 5 × 10 − 6 5×10^{-6} 5 × 1 0 − 6 10 − 6 10^{-6} 1 0 − 6 L 2 L^2 L 2 1500 × 1500 1500×1500 1500 × 1500 ( 28 ) (28) ( 28 ) ( 29 ) (29) ( 29 ) ( 30 ) (30) ( 30 ) ( 31 ) (31) ( 31 )
值得注意的是,在湍流通道流问题(即第三和第四测试案例)中,TSA-PINN 和标准 PINN 的训练时长保持相同。在此限制下,标准 PINN 能够完成约 25%的训练周期。尽管如此,TSA-PINN 持续优于标准版本,展现出更优的性能。
图 13 展示了瞬时速度场与参考 DNS 解和 TSA-PINN 预测的三个不同时间段的比较。这些比较表明,TSAPINN 的近似值与参考解相符,尤其是在早期阶段。由于初始条件在第一个时间框架中规定,准确性初期较好,但随着时间推移通常会下降。这一观察结果在表 4 中得到了证实,表 4 也清楚地显示了 TSA-PINN 相较于标准 PINN 的优越效率。此外,分析了 TSA-PINN 在捕捉近壁现象(粘性子层、缓冲区和对数定律区)方面的性能。图 14 展示了 TSA-PINN 对平均速度剖面的近似如何对应近壁区域的预期行为。定量结果显示,模型在 y + = 10 y^+ = 10 y + = 10 U + = y + U^+ = y^+ U + = y + 10 < y + < 30 10<y^+<30 10 < y + < 30 y + > 30 y^+>30 y + > 30
三维时间相关湍流通道流动:覆盖更大范围
作为案例 4 的延伸,这个最终验证和测试场景(案例 5)涉及一个显著更大的域,覆盖了信道高度的一半。该子域 [ 12.47 , 12.66 ] × [ − 1.00 , − 0.0031 ] × [ 4.61 , 4.82 ] [12.47,12.66] × [−1.00,−0.0031] × [4.61,4.82] [ 12.47 , 12.66 ] × [ − 1.00 , − 0.0031 ] × [ 4.61 , 4.82 ] x x x y y y z z z 40 , 000 40,000 40 , 000 26 , 048 26,048 26 , 048 147 , 968 147,968 147 , 968 10 10 10 300 300 300 100 100 100 10 − 3 10^{-3} 1 0 − 3 10 − 4 10^{-4} 1 0 − 4 250 250 250 10 − 5 10^{-5} 1 0 − 5 250 250 250 5 × 10 − 6 5×10^{-6} 5 × 1 0 − 6 150 150 150 10 − 6 10^{-6} 1 0 ��− 6
值得一提的是,壁面法线和跨度方向的速度相比流速表现出更大的相对 L 2 L^2 L 2 t = 12 × 0.0065 t = 12 × 0.0065 t = 12 × 0.0065 t ∈ [ 0 , 8 × 0.0065 ] t \in [0, 8 × 0.0065] t ∈ [ 0 , 8 × 0.0065 ]
图 16 和表 5 定量证实了这一观察,将模型数值近似相关的误差 L 2 L^2 L 2 u u u 10 − 3 10^{-3} 1 0 − 3 v v v w w w 10 − 2 10^{-2} 1 0 − 2 0.06 0.06 0.06
在本研究中,我们引入了一种变革性方法,利用一种新颖的物理知情神经网络模型,结合可训练正弦激活函数(TSA-PINN)来近似纳维-斯托克斯方程的解。我们方法的核心是整合创新的可训练神经元正弦激活机制和动态斜坡恢复机制。激活频率与目标函数的初始对齐,加上其可训练特性,使得训练期间能够持续优化,确保模型动态收敛至最优设置。坡度恢复机制是我们模型的补充,实时调整激活函数的频率,稳定梯度流动,防止梯度消失或爆炸等问题。这导致收敛速度更快,增强模型的稳健性。我们的数值实验涵盖了从稳态二维到高雷诺数的时变三维湍流。在第一次和第二次验证实验中——盖子驱动的腔体流动,R e = 100 Re = 100 R e = 100 R e = 3200 Re = 3200 R e = 3200