Skip to main content

谱方法

谱方法（Spectral Method）起源于 20 世纪 60 年代，最早由 Orszag 等人提出并系统化，用于求解流体力学和气象学中的偏微分方程问题。其核心思想是将待求解函数展开为一组全局正交基函数（如 Fourier 三角函数或 Legendre、Chebyshev 多项式）的线性组合，通过求解系数来近似原函数的解。这种方法与传统的有限差分方法（Finite Difference Method, FDM）和有限元方法（Finite Element Method, FEM）有本质区别：有限差分方法通常通过局部网格点的函数值逼近导数，有限元方法通过局部分片多项式近似解，而谱方法采用全局展开，使得在求解平滑问题时可以达到指数级收敛（spectral accuracy），在相同的自由度下精度远超传统方法。

由于其高精度和计算效率，谱方法在求解光滑解的偏微分方程、流体力学、波动方程以及量子力学等领域得到广泛应用。近年来，随着数值线性代数和高性能计算的发展，谱方法逐渐成为求解高维复杂问题的重要工具，为科学计算提供了一种与传统方法互补的新途径。

本网页内容主要参考了两本谱方法领域的重要著作：Lloyd N. Trefethen 的 Spectral Methods in MATLAB（2000），系统介绍了谱方法的基本理论与 MATLAB 实现；以及 Jie Shen、Tao Tang 和 Li-Lian Wang 合著的 Spectral Methods: Algorithms, Analysis and Applications（2011），详细讨论了谱方法的算法设计、误差分析及在偏微分方程中的应用。基于这两本书，本文将对谱方法的理论背景、数值实现及应用进行简明介绍。

Spectral Methods: Algorithms, Analysis and Applications（2011）

图 1：Spectral Methods: Algorithms, Analysis and Applications（2011）

Spectral Methods in MATLAB（2000）

图 2：Spectral Methods in MATLAB（2000）

我们先来阅读 Spectral Methods in MATLAB（2000），因为这本书比较基础，Spectral Methods: Algorithms, Analysis and Applications（2011）阅读起来会比较困难，他适合有一定计算数学基础的人阅读。

Chapter 1 微分矩阵​

我们的出发点是一个基本问题。给定一组网格点 {xj}\{x_j\} 和相应的函数值 {u(xj)}\{u(x_j)\}，我们如何使用这些数据来近似 uu 的导数？可能立即想到的方法是某种有限差异公式。正是通过有限差分格式，这是谱方法的动机。

考虑均匀网格 {x1,…,xN}\{x_1,\dots,x_N\} ，每个 jj 的 xj+1−xj=hx_{j+1} - x_j = h，以及一组对应的数据值 {u1,…,uN}\{u_1,\dots,u_N\}：

让 wjw_j 表示 u′(xj)u\prime(x_j) 的近似值，即 xjx_j 处的 uu 的导数。标准的二阶恒距近似值为

wj=uj+1−uj−12h,(1.1)w_j=\frac{u_{j+1}-u_{j-1}}{2h},\tag{1.1}

这可以通过考虑 u(xj+1)u(x_{j+1}) 和 u(xj−1)u(x_{j-1}) 的泰勒展开来推导。为简单起见，让我们假设问题是周期性的，并取 u0=uNu_0 = u_N 和 u1=uN+1u_1 = u_{N+1}。然后我们可以将离散二叶化过程表示为矩阵-向量乘法，有

(w1⋮wN)=h−1(012−12−120⋱⋱⋱01212−120)(u1⋮uN).(1.2)\left(\begin{array}{c}w_{1}\\ \\ \\ \vdots\\ \\ w_{N}\end{array}\right) = h^{-1}\left(\begin{array}{ccccc}0&\frac{1} {2}&&&-\frac{1}{2}\\ -\frac{1}{2}&0&&\ddots&&\\ &&&\ddots&&\\ &&&\ddots&0&\frac{1}{2}\\ \frac{1}{2}&&&-\frac{1}{2}&0\end{array}\right)\left(\begin{array}{c}u_{1}\\ \\ \\ \vdots\\ \\ u_{N}\end{array}\right). \tag{1.2}

（此处和本书中其他稀疏矩阵中省略的条目为零。观察该矩阵是 Toeplitz 矩阵，沿对角线具有恒定的条目，即 aija_{ij} 仅依赖于 ii 和 jj 。事实上，它也是循环的，这意味着 aija_{ij} 仅依赖于 ii 和 jj (modN)(mod N )。对角线“环绕”矩阵。

推导 (1.1) 和 (1.2) 的另一种方法是通过以下局部插值和分配过程：

For j=1,2,...,Nj=1,2,...,N

  • 设 pjp_j 是 pj（xj−1）=uj−1,pj（xj）=uj,pj（xj+1）=uj+1p_j（x_{j-1}） = u_{j-1},p_j（x_j） = u_j,p_j（x_{j+1}）= u_{j+1} 的次数 ≤2 次唯一多项式。
  • 设 wj=p′j(xj)w_j=p\prime_j(x_j)

很容易得到，对于固定的 jj ，插值 pjp_j 由下式给出

pj(x)=uj−1a−1(x)+uja0(x)+uj+1a1(x),p_{j}(x)=u_{j-1} a_{-1}(x)+u_{j} a_{0}(x)+u_{j+1} a_{1}(x),

其中， a−1(x)=(x−xj)(x−xj+1)/2h2,a0(x)=−(x−xj−1)(x−xj+1)/h2a_{-1}(x) = (x - x_{j})(x - x_{j+1}) / 2 h^{2}, a₀(x) = -(x-x_{j-1})(x-x_{j+1}) / h², 以及 a1(x)=(x−xj−1)(x−xj)/2h2a₁(x) = (x-x_{j-1})(x-x_j) / 2 h². 对数式求导并在 x=xjx=x_{j} 处取值，即可得到 (1.1)(1.1)。

同理可以得到四阶矩阵为

(w1⋮wN)=h−1(⋱112−23⋱−112112⋱23⋱⋱0⋱⋱−23⋱−112112⋱23−112⋱)(u1⋮uN).(1.3)\left(\begin{array}{c}w_{1}\\ \\ \\ \\ \vdots\\ \\ \\ \\ w_{N}\end{array}\right) = h^{-1}\left(\begin{array}{ccccc}&&\ddots&& \frac{1}{12}&-\frac{2}{3}\\ &&\ddots-\frac{1}{12}&&&\frac{1}{12}\\ &&\ddots&\frac{2}{3}&\ddots&\\ &&\ddots&0&\ddots&\\ &&\ddots&-\frac{2}{3}&\ddots&\\ -\frac{1}{12}&&&\frac{1}{12}&\ddots&\\ \frac{2}{3}&-\frac{1}{12}&&&\ddots&\\ \end{array}\right) \left(\begin{array}{c}u_{1}\\ \\ \\ \\ \vdots\\ \\ \\ u_{N}\end{array}\right).\tag{1.3}

这次我们有一个五对角线而不是三对角线循环矩阵。 (1.2)和(1.3)的矩阵是二元化矩阵的例子。它们的精度分别为二级和四级。也就是说，对于通过对光滑函数 uu 进行采样获得的数据 uju_j，与 u′(xj)u\prime(x_j) 的相应离散近似值将以速率 O(h2)O(h^2) 和 O(h4)O(h^4) 收敛为当 h→0h\to0。可以通过考虑泰勒级数来验证这一点。 我们的第一个 Matlab 程序，Program 1，说明了 (1.3) 的行为。

实验一​

我们取 u(x)=esin(x),u′(x)=cos(x)esin(x)u(x) = e^{sin(x)},u\prime(x)=cos(x)e^{sin(x)} 并给出域 [−π;π][-\pi ;\pi ] 的周期性数据：

因为它使用了 Matlab 稀疏矩阵，所以这段代码在工作站上运行的时间只有几分之一秒，即使它作的维度高达 4096 的矩阵 [GMS92]。结果显示在输出 1 中，它绘制了网格上针对 N 的最大误差。四阶精度是显而易见的。这是我们第一个也是最后一个没有说明谱方法的例子！

我对书中谱方法的例子经过图例的改良得到以下程序：

% p1.m - convergence of fourth-order finite differences
e = exp(1);
Nvec = 2.^(3:12);

% 创建大尺寸 figure (单位：像素)
figure('Color','w','Position',[100 100 700 700])
ax = axes(); % 左下角x,y,width,height

for N = Nvec
    h = 2*pi/N;
    x = -pi + (1:N)'*h;
    u = exp(sin(x));
    uprime = cos(x).*u;

    % Construct sparse 4th-order differentiation matrix
    e1 = ones(N,1);
    D = sparse(1:N,[2:N 1],2*e1/3,N,N) - sparse(1:N,[3:N 1 2],e1/12,N,N);
    D = (D-D')/h;

    % Compute error
    error = norm(D*u-uprime,inf);
    loglog(N,error,'.','markersize',15), hold on
end

grid on
xlabel('N','FontSize',20,'FontName','Times New Roman')
ylabel('error','FontSize',20,'FontName','Times New Roman')
title('Convergence of 4th-order finite differences','FontSize',20,'FontName','Times New Roman')
semilogy(Nvec,Nvec.^(-4),'--')
text(105,5e-8,'N^{-4}','FontSize',20,'FontName','Times New Roman')

set(ax,'FontSize',20,'FontName','Times New Roman')
axis square % 保持坐标轴为正方形比例

% 保存高清图片，占满画布
exportgraphics(gcf,'p1.png','Resolution',300)

结果可见图 3

实验二​

我们已经研究了二阶和四阶的二阶，很明显，考虑六阶、八阶和更高阶方案将导致带宽增加的循环矩阵。谱方法背后的想法是将这个过程发挥到极限，至少在原则上是这样，并使用无限阶和无限带宽的双分公式(即密集矩阵)[For75]。在下一章中，我们将证明在这个极限下，对于无限等距网格，人们得到以下无限矩阵：

D = h−1(⋮⋱13⋱−12⋱10−1⋱12⋱−13⋱⋮).(1.4)D\ =\ h^{-1}\left(\begin{array}{ccccccccc}&&&&&\vdots&&&&\\ &&&&\ddots&&&&\frac{1}{3}&&&&\\ &&&&\ddots&&&&-\frac{1}{2}&&&&\\ &&&&\ddots&&&&1&&&&\\ &&&&&&&0&&&&\\ &&&&&&&-1&&&&\ddots&&\\ &&&&&&&\frac{1}{2}&&&&\ddots&&\\ &&&&&&-\frac{1}{3}&&&&\ddots&\\ &&&&&&&\vdots&&&&\end{array}\right).\tag{1.4}

这是有限托普利茨矩阵中双重偏对称 (DT=DD^T = D)，也称为洛朗算子 [Hal74，Wid65]。除主对角线上的条目外，其所有条目都是非零的。

当然，在实践中，人们不使用有限矩阵。对于有限网格，以下是 spectral collocation methods 的设计原则：

  • 设 pp 是一个函数(独立于 jj )，使得所有 jj 的 p(xj)=ujp(x_j) = u_j。
  • 设 wj=p′(xj)w_j=p\prime(x_j)。

我们可以自由选择 pp 来解决手头的问题。对于周期域，自然选择是等距网格上的三角多项式，由此产生的“Fourier”方法将在第 4 章和后面的章节中断断续续地关注。对于非周期域，不规则网格上的代数多项式是正确的选择，我们将从第 5 章和第 6 章开始描述这种类型的“Chebyshev”方法。（这部分内容包括矩阵(1.5)先按下不表，后面的内容学习以后就会明白）

对于有限 N，即使为了简单起见，也取 N，这是我们将在第 3 章中推导的周期性规则网格的 N×NN×N 密集矩阵

DN=(⋱⋮⋱12cot⁡3h2⋱−12cot⁡2h212cot⁡1h20−12cot⁡1h2⋱12cot⁡2h2⋱−12cot⁡3h2⋱).(1.5) D_{N}=\left(\begin{array}{cccc} & \ddots & \vdots & \\ \ddots & \frac{1}{2} \cot \frac{3 h}{2} & & \\ \ddots & -\frac{1}{2} \cot \frac{2 h}{2} & & \\ & \frac{1}{2} \cot \frac{1 h}{2} & & \\ & & 0 & \\ & & -\frac{1}{2} \cot \frac{1 h}{2} & \ddots \\ & \frac{1}{2} \cot \frac{2 h}{2} & \ddots \\ & & -\frac{1}{2} \cot \frac{3 h}{2} & \ddots \end{array}\right) .\tag{1.5} 
% p2.m - convergence of periodic spectral method (compare p1.m)
e = exp(1);

% 创建大尺寸 figure
figure('Color','w','Position',[100 100 700 700])
clf

% 坐标轴占满整个图像
ax = axes(); % 左下角x,y,width,height

for N = 2:2:100
    h = 2*pi/N;
    x = -pi + (1:N)'*h;
    u = exp(sin(x));
    uprime = cos(x).*u;

    % Construct spectral differentiation matrix
    column = [0 .5*(-1).^(1:N-1).*cot((1:N-1)*h/2)];
    D = toeplitz(column,column([1 N:-1:2]));

    % Compute error
    error = norm(D*u-uprime,inf);
    loglog(N,error,'.','markersize',15), hold on
end

grid on
xlabel('N','FontSize',20,'FontName','Times New Roman')
ylabel('error','FontSize',20,'FontName','Times New Roman')
title('Convergence of spectral differentiation','FontSize',20,'FontName','Times New Roman')

set(ax,'FontSize',20,'FontName','Times New Roman')
axis square

% 保存高清 PNG，占满画布内容
exportgraphics(gcf,'p2.png','Resolution',600)

Program 2 与 Program 1 相同，只是 (1.3) 替换为 (1.5)。它对结果的影响是多么不同啊！图 4 中的误差会迅速减少，直到达到如此高的精度，以至于计算机上的舍入误差阻止了任何进一步的改进。这种显着的行为称为 spectral accuracy"。我们将在第 4 章中对这句话进行一些精确性，但目前需要注意的一点是它与有限方法和有限元方法的收敛率有多么不同。随着 NN 的增加，有限二元或有限元方案中的误差通常会像某个常数 mm 的 O(N−m)O(N^{-m}) 一样减小，这取决于近似阶数和解的平滑度。对于光谱方法，只要解是可精确的，则每 mm 的速率 O(N−m)O(N^{-m}) 可以实现收敛，并且如果解是适当的解析，则以速率 O(cN)(0<c<1)O(c^N )(0 < c < 1) 实现更快的收敛。

我们描述的矩阵已经流传。循环矩阵的作用是卷积，正如我们将在第 3 章中看到的，卷积可以使用离散傅里叶变换来计算。从历史上看，正是 1965 年针对此类问题的快速傅里叶变换 （FFT） 的发现导致了 1970 年代人们对谱方法的兴趣激增。我们将在第 8 章中看到，FFT 不仅适用于等距网格上的三角多项式，也适用于切比雪夫网格上的代数多项式。然而，在没有 FFT 的情况下实现的频谱方法也很强大，在许多应用中，使用显式矩阵是相当令人满意的。本书中的大多数问题都是通过矩阵解决的。

Adams-Bashforth方法数值解比较

图 3：四阶有限差分的收敛性

Adams-Moulton方法数值解比较

图 4：error：谱法 （1.5） 的 “Spectral accuracy”，直到舍入误差接管 10−1410^ {-14} 左右。现在矩阵很密集，但 N 的值比程序 1 中的值小得多。

Chapter 2 无界网格：半离散傅里叶变换​

我们现在推导出第一个谱方法，该方案适用于一个离散的无限域。因此不是一个实用的方法，但是它确定了我们接下来看到的实用方案的推导和分析的数学思想。

我们的无限网格用 hZh\mathbb{Z} 表示，网格中有 xj=jh,j∈Zx_j=jh,j\in \mathbb{Z}。这是所有整数集合：

我们将根据半离散傅里叶和带限制的 Sinc 函数插值的关键思想得出(1.4)，在离散之前，我们会考虑连续案例。函数 u(x),x∈Ru(x),x \in \mathbb{R} 的傅里叶变换由函数 u^(k)\hat{u}(k) 定义的：

u^(k)=∫−∞∞e−ikxu(x)dx,k∈R.(2.1)\hat{u}(k)=\int_{-\infty}^{\infty}e^{-\mathit{ikx}}u(x) dx,\qquad k\in \mathbb{R}.\tag{2.1}

u^(k)\hat{u}(k) 可以理解为“在波数 kk 处的 uu 的振幅密度”，将函数分解到其组成波中的过程叫 "傅里叶变换"

相反，我们可以通过逆傅里叶变换从 u^\hat{u} 重建 uu ，有

u(x)=12π∫−∞∞eikxu^(k)dk,x∈R.(2.2)u(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{\mathit{ikx}} \hat{u}(k) dk, \qquad x\in \mathbb{R}. \tag{2.2}

这里“傅里叶合成”变量 x 是物理变量，k 是傅里叶变量或波数。

我们想考虑 xx 在 hZh\mathbb{Z} 上而不是 RR 范围内，傅里叶变换的精确解和它的反问题存在。关键在于，由于空间结构域是离散的，因此波数 k 将不再范围在所有 R\mathbb{R} 上，kk 是有限的，因为 xx 是离散的；

物理空间： 离散， 无限 : x∈hRx \in h\mathbb{R}

傅里叶空间： 有界， 连续 : k∈[−π/h,π/h]k \in [-\pi / h , \pi / h]

这些关联的成因在于一种称为混叠的现象。当 k1≠k2k_1 ≠ k_2 时，两个复指数函数 f(x)=exp(ik1x)f(x) = exp(ik_1x) 与 g(x)=exp(ik2x)g(x) = exp(ik_2x) 在实数域 R\mathbb{R} 上不相等。然而若将函数限制在 hZh\mathbb{Z} 网格上，它们分别取值为 fj=exp(ik1xj)f_j = exp(ik_1x_j) 和 gj=exp(ik2xj)g_j = exp(ik_2x_j) 。当 k1k_1 和 k2k_2 是 2π/h2\pi /h 的整数倍时，则对任意 jj 均有 fj=gjf_j = g_j。由此可知，对于任意复指数函数 exp(ikx)exp(ikx) ，在 kk 的 hZh\mathbb{Z} 网格上存在无限多个与其匹配的复指数函数。因此只需在长度为 2π/h2\pi/h 的区间内测量该网格的波数，基于对称性考虑，我们选取区间 [−π/h,π/h][-\pi/h, \pi/h] 。

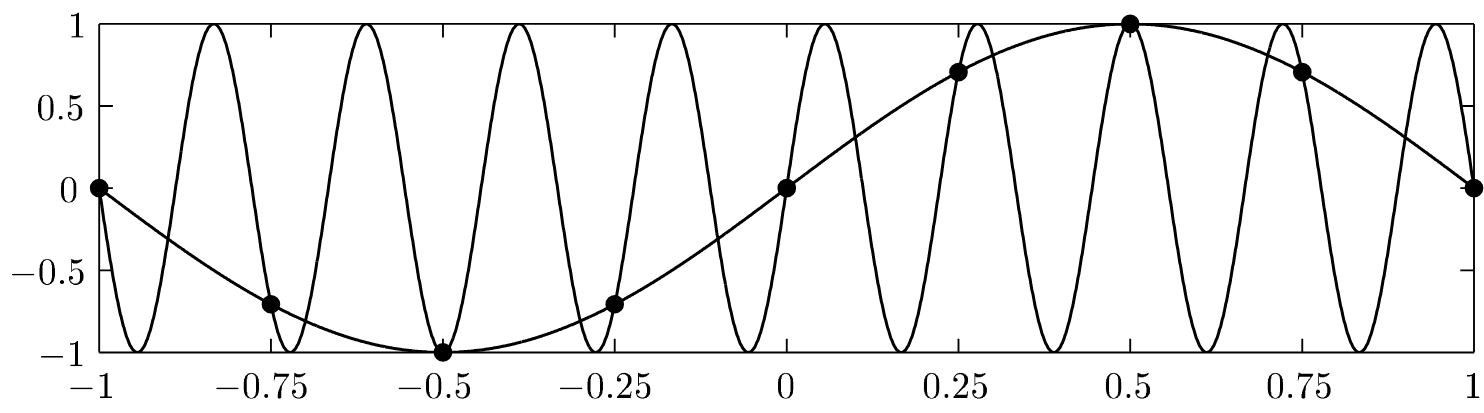
图 5 说明了函数 sin(x)sin(x) 和 sin(9x)sin(9x) 的混叠，点表示对网格 14Z\frac{1}{4}\mathbb{Z} 的限制，其中这两个函数值是相同的。

对于在 xjx_j 处用值 vjv_j 在 hZh\mathbb{Z} 上定义的函数 vjv_j，半离散的傅里叶变换是由

v^(k)=h∑j=−∞∞e−ikxjvj,k∈[−π/h,π/h],(2.3)\hat{v}(k)=h\sum_{j=-\infty}^{\infty}e^{-\mathit{ikx}_{j}}v_{j},\qquad k\in[- \pi/h,\pi/h],\tag{2.3}

和反向半离散傅里叶变换是

vj=12π∫−π/hπ/heikxjv^(k)dk,j∈Z.(2.4)v_{j}=\frac{1}{2\pi}\int_{-\pi/h}^{\pi/h}e^{\mathit{ikx}_{j}}\hat{v}(k) dk, \qquad j\in \mathbb{Z}.\tag{2.4}

注意：(2.3) 通过梯形规则近似 (2.1) ，而(2.4)通过将 R\mathbb{R} 截断为 [−π/h,π/h][-\pi/h,\pi/h]。当h→0h \to 0 时两公式相等。

对于不同的谱频，我们需要一个插值，而反变形 (2.4) 为我们提供一个。我们要做的是评估 x∈Rx\in \mathbb{R} 相同的公式。不仅仅是 xj∈hZx_j \in h \mathbb{Z} ，也就是说，在确定 v^\hat{v} 之后，我们通过

p(x)=12π∫−π/ℏπ/ℏeikxv^(k)dk,x∈R.(2.5)p(x)=\frac{1}{2\pi}\int_{-\pi/\hbar}^{\pi/\hbar}e^{\mathit{ikx}} \hat{v}(k) \mathit{d}k,\qquad x\in\mathbb{R}.\tag{2.5}

这是每个 jj 的 x 的分析函数。此外，通过构造，由定义傅里叶变换 p^\hat{p} ，有

p^(k)={v^(k)k∈[−π/h,π/h],0otherwise.\hat{p}(k)=\left\{\begin{aligned} & \hat{v}(k)&& k\in[-\pi/h,\pi/h],\\ & 0&&\text{otherwise}.\end{aligned}\right.

因此, p^\hat{p} 在区间 [−π/h,π/h][-\pi/h,\pi/h] 上具有紧凑的支撑集。我们称 pp 是 vv 的带限插值函数，这不仅意味着 p^\hat{p} 具有紧支集，更意味着该支集被限定在特定区间 [−π/h,π/h][-\pi/h,\pi/h] 内。尽管任意网格函数可能存在无穷多个插值函数，但按此定义仅存在唯一的带限插值函数。

我们给出对 hZh\mathbb{Z} 定义的函数 vv 的谱微分的前两个描述，有

  • 给定 vv ，通过(2.5) 确定其带限的插值 pp 。
  • 设 wj=p′(xj)w_j = p \prime (x_j)

另一个通过傅里叶空间可获得，如果 uu 是具有傅里叶变换 u^\hat{u} 的可区分函数，则 u′u\prime 的傅里叶变换是 iku^(k)ik\hat{u}(k):

u′^(k)=iku^(k).(2.6)\widehat{u^{\prime}}(k) = ik \hat{u}(k).\tag{2.6}

可以通过相对于 xx 区分(2.2)或(2.5)来获得此结果。因此，我们有一个系数的谱微分：

  • 给定 vv ，计算其半离散傅里叶变换 v^\hat{v} 用(2.3)。

  • 定义 w^(k)=ikv^(k)\hat{w}(k)=ik\hat{v}(k) 。

  • 根据 (2.4)式计算 ww 的值为 w^\hat{w} 。

这两个对谱不同描述在数学上是完整的，但我们尚未得出矩阵的系数(1.4)。为此，我们可以使用傅里叶变换来返回并深入了解带限制的插值 p(x)p(x) ，令 kronecker-delta 函数：

δj={1j=0,0j≠0.(2.7)\delta_{j}=\left\{\begin{aligned} 1&\quad j=0,\\ 0&\quad j\neq 0.\end{aligned}\right.\tag{2.7}

根据(2.3)， δ\delta 的半离散傅里叶变换为常数：δ^(k)=h\hat{\delta}(k)=h，对所有 k∈[−π/h,π/h]k\in[-\pi/h,\pi/h]。根据(2.5)，δ\delta 的带限插值函数相应为

p(x) = h2π∫−π/hπ/heikxdk = sin⁡(πx/h)πx/hp(x)\ =\ \frac{h}{2\pi}\int_{-\pi/h}^{\pi/h}e^{\mathit{ikx}} dk\ =\ \frac{\sin(\pi x/h)}{\pi x/h}

(x=0 的插值为 1)，这个著名的功能称为 Sinc 功能：

Sℏ(x)=sin⁡(πx/h)πx/h.(2.8)S_{\hbar}(x)=\frac{\sin(\pi x/h)}{\pi x/h}.\tag{2.8}

带限插值本质上是一种平移不变的过程，具体而言，对于任意 mm，δj−m\delta_{j-m} 的带限插值是 Sh(x−xm)S_h(x-x_m)。一般网格函数 vv 可表示为：

vj=∑m=−∞∞vmδj−m,(2.9)v_{j}=\sum_{m=-\infty}^{\infty}v_{m}\delta_{j-m},\tag{2.9}

因此根据半离散傅里叶变换的线性性质，可知 vv 的带限插值函数是平移 Sinc 函数的线性组合：

p(x)=∑m=−∞∞vmSℏ(x−xm).(2.10)p(x)=\sum_{m=-\infty}^{\infty}v_{m}S_{\hbar}(x-x_{m}).\tag{2.10}

导数相应为

wj=p′(xj)=∑m=−∞∞vmSh′(xj−xm).(2.11)w_{j}=p^{\prime}(x_{j})=\sum_{m=-\infty}^{\infty}v_{m}S^{\prime}_{h}(x_{j}-x_{ m}).\tag{2.11}

现在我们推导式(1.4)中双无限托普利茨矩阵 D 的元素。若将式(2.11)视为式(1.5)中的矩阵方程，可知向量 Sh′(xj)S^{'}_h(x_j) 即为 DD 的第 m=0m=0 列，其余列可通过适当上移或下移该列获得。式(1.4)的元素由微积分习题确定：对式(2.8)求导可得

Sh′(xj)={0j=0,(−1)jjhj≠0.(2.12)S_{h}^{\prime}(x_{j})=\left\{\begin{aligned} & 0&& j=0,\\ & \frac{(-1)^{j}}{jh}&& j\neq 0.\end{aligned}\right.\tag{2.12} 
% p3.m - band-limited interpolation
h = 1; xmax = 10; clf
x = -xmax:h:xmax; % computational grid
xx = -xmax-h/20:h/10:xmax+h/20; % plotting grid

figure('Position',[100 100 800 500]); % 调大图像窗口

for plt = 1:3
    subplot(3,1,plt)
    switch plt
        case 1, v = (x==0); % delta function
        case 2, v = (abs(x)<=3); % square wave
        case 3, v = max(0,1-abs(x)/3); % hat function
    end
    plot(x,v,'.','markersize',14), grid on
    p = zeros(size(xx));
    for i = 1:length(x)
        p = p + v(i)*sin(pi*(xx-x(i))/h)./(pi*(xx-x(i))/h);
    end
    line(xx,p,'linewidth',.7), axis([-xmax xmax -.5 1.5])
    set(gca,'xtick',[],'ytick',[0 1])
    set(gca,'FontName','Times New Roman','FontSize',20)
end

% 设置整体标题
sgtitle('Band-limited Interpolation','FontName','Times New Roman','FontSize',20)
saveas(gcf,'p3.png')

图 6：三种网格函数的带限插值；首个插值函数为 sinc 函数 Sh(x)S_h(x)。此类插值函数是谱方法的基础，但这些示例不够光滑，无法实现高精度。

Chapter 3 周期性网格：密度泛函理论(DFT)与快速傅里叶变换(FFT)​

现在，我们转向有限的周期性网格上的谱分化。该过程以等式（1.5）的 n n 矩阵操作的形式说明。最后一章介绍了与无限网格 Hz 相对应的无限矩阵（1.4），但本章制定了一个实用的计算方案。从数学上讲，这两个方案之间存在密切的连接，我们的光谱方法的推导将与以前相同。不同之处在于，半混凝土傅立叶变换被离散的傅立叶变换（DFT）取代，可以通过快速傅立叶变换（FFT）计算。