微分方程数值解法

单步方法

Euler 法

对于初值问题(1)

\left\{ \begin{aligned} &{u}'=f(t,u), t_0<t \le T, \\ &u(t_0)=a, \end{aligned} \right.

我们并不试图在自变量的整个连续区间上去逼近精确解 $u(t)$ , 只是在 $N$ 个离散点 $\{t_m\}^N_{m=1}$ 上考虑近似解 $\{U_m\}^N_{m=1}$ , 这里 $t_1,t_2,...,t_N \le T$ 称为 N 个节点, 它们满足关系

t_{m+1}=t_m + h_{m+1},m=0,1,...,N-1,

$\{h_m\}^N_{m=1}$ 是一组被称为步长的正数(如果当 $h_m=h=C,C为常数$ ，这组结点被称为等步长的)。

Euler 方法是通过斜率来研究的，因为斜率已经给出了，当 $h$ 很小的时候，用过 (t_0,u_0)的点斜式直线方程在 $t_1$ 处的值 $u_1$ 来近似代替 $u(t_1)$ ，即

\frac{u_1-u_0}{t_1-t_0} = f(t_0,u_0),

由于这时 $h=t_1-t_0$ ，所以公式可以转换成

u_1 = u_0 + hf(t_0,u_0),

得到 $u_1$ 之后，由于 $t_1$ 是知道的，又可以推出 $u_2$ 。以此类推，得到 $\{u_m\}^N_{m=1}$ 的递推公式：

\left\{ \begin{aligned} &u_{m+1}=u_m+hf(t_m,u_m), m=0,1,...,N-1, \\ &u_0=u(t_0)=a, \end{aligned} \right.

上述方法就是 Euler 方法，也称 Euler-Cauchy 折线法。

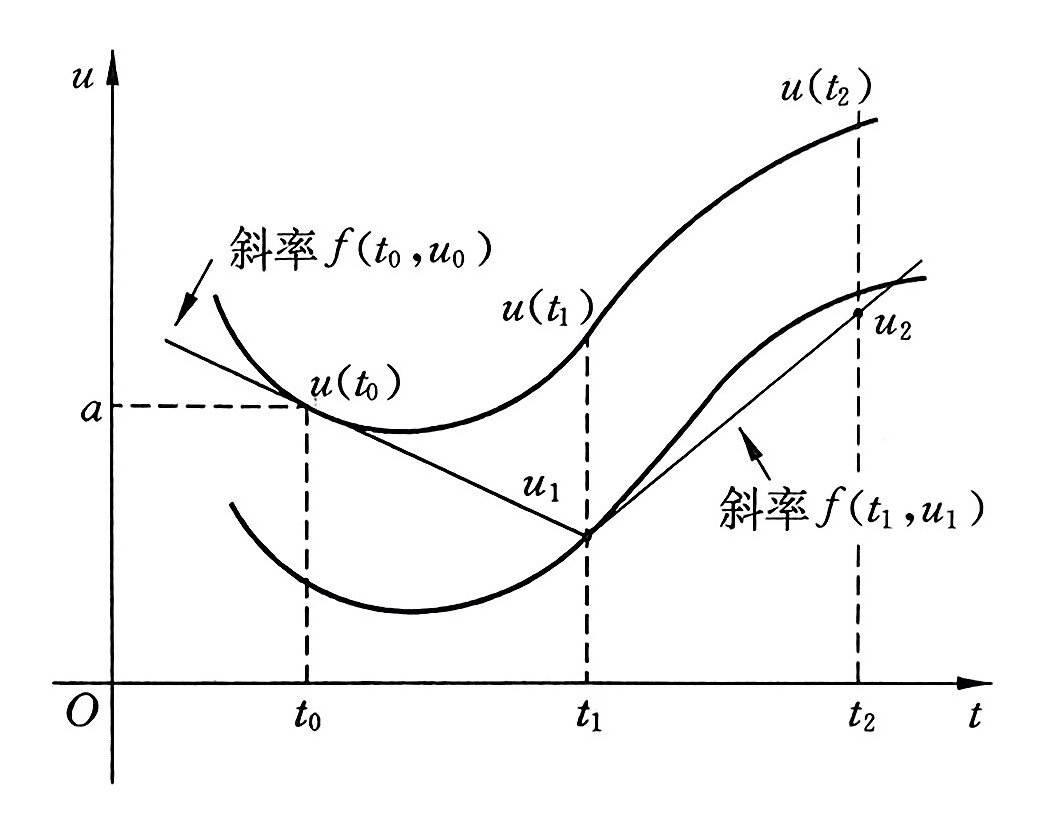
图 1：示意图

对于 Euler 方法可以有三种不同的解释：

(1) 数值微分：用最简单的向前差商 $\frac{u(t+h)-u(t)}{h}$ 来近似代替 ${u}'(t)$ ，即有

u(t+h)\approx u(t)+hf(t,u(t)),

(2) 数值积分：在 $[t,t+h]$ 对方程(1)两端积分，并采用左矩形公式，有

u(t+h)-u(t)=\int^{t+h}_tf(\tau,u(\tau))d\tau \approx hf(t,u(t)),

(3) 幂级数展开：将 $u(t+h)$ 在 $t$ 作 Taylor 展开，并略去 $h^2$ 以上的项，有

u(t+h) = u(t)+hu'(t)+\frac{h^2}{2!}u''(t)+\cdots \approx u(t)+hf(t,u(t)),

在以上三式中令 $t=t_m$ ，并用 $t_m$ 记 $u(t_m)$ 的近似值。

算例 1

用 Euler 方法解初值问题

\left\{ \begin{aligned} &u'=u-\frac{2t}{u},0<t\le1 \\ &u_0=1, \end{aligned} \right.

它的真解为 $u(t)=\sqrt{1+2t}$ ，设定步长公式为 $h^{(i)}=\frac{1}{2^{4i}},(i=1,2),h^{(3)}=\frac{1}{2^{10}}$ (h 取为 $2^{-n}$ 形式可避免计算步长时的误差)，则 $t^{(i)}_m=mh^{(i)}$ ，用 Euler 公式，有

u^{(i)}_{m+1} = u^{(i)}_{m} + h^{(i)}(u^{(i)}_m-\frac{2mh^{(i)}}{u^{(i)}_m}).

下面我们来进行实验

这是使用了 Euler 最基本的方法对应上面提到的(1) 数值微分

这是使用了 Euler 进阶一点的方法对应上面提到的(2) 数值积分

这是使用了 Euler 进阶一点的方法对应上面提到的(3) 幂级数展开（只到二阶）

三种方法在耗时以及误差上的比较,可以看出最耗时间是积分法，幂级数展开法（二阶）与微分法差别不大：

多步法

显式方法和隐式方法

等式右端不含有 $u_{m+1}$ ,即只要通过递推就可以获得 $u_{m+1}$ ,这种方法是显示的。

但是有些方法不能显式地输出 $u_{m+1}$ ，如果对方程两端在 $[t_,,t_m+h]$ 上积分，并用梯形公式来近似，则有

u(t_{m+1})-u(t_m) = \int^{t_m+h}_{t_m}f(\tau,u(\tau)) d\tau, \\ \approx \frac{h}{2} [f(t_m,u(t_m))+f(t_{m+1},u(t_{m+1}))],

可以得到著名的改进 Euler 法：

\left\{ \begin{aligned} &u_{m+1}=u_m+\frac{h}{2} [f(t_m,u_m)+f(t_{m+1},u(t_{m+1}))],m=0,1,\dots,N-1, \\ &u_0=a, \end{aligned} \right.

先验误差

一般来说，即使 $u_m$ 精确地等于 $u(t_m)$ ，算出的 $u_{m+1}$ 一般也不会等于 $u(t_{m+1})$ ，这是方程的换算并非精确的，因此这个误差也就是近似格式对方程离散所产生的误差，我们称为局部截断误差，记为 $R_m$ 。

于是 $R_m$ 为精确值 $u(t_{m+1})$ 与 $u_{m+1}$ 的差，用近似格式算出的 $u(t_{m+1})$ 的近似值，即

R_m = u(t_{m+1}) - u_{m+1} = u(t_{m+1}) - [u(t_m)+h \varphi (t_m,u(t_m);h) ].

因此， $R_m$ 也可以看成用精确值代替近似值后左端减去右端的差。

同样，我们可以导出线性多步方法的局部截断误差：

R_m = \sum ^k _{j=0} \alpha_j u(t_m +jh) -h\sum^k_{j=0}\beta_j f(t_m+jh,u(t_m+jh)).

由于，事实上 $u_m$ 决不会精确地等于 $u(t_m)$ ，所以总的误差应该是前面已经产生地误差与某种积累与本次所产生的误差的一个合并效应。

所以，整体截断误差应为式之间所产生的误差为

\varepsilon_m = u(t_m) -u_m

定理 2.3 若 $f(t,u)$ 在 G 上分别关于 $t,u$ 满足 Lipschitz 条件，相应的 Lipschitz 常数分别为 $K$ 和 $L$ ，则 Euler 方法的整体截断误差的上界满足估计式

\varepsilon < \frac{K+LM_1}{2L}(e^{L(T-t_0)}-1)h, (2)

也即 Euler 方法是一阶收敛的。

像这样不首先确定近似解就由所讨论问题的数据直接估计出的（原则上的）误差界称为先验误差界。

当 $f(t,u)$ 关于 $t,u$ 的偏导数分别存在时，可以取

M_1= \max_{t_0 \le t \le T}|u'(t)|=\max_{t_0 \le t \le T}|f(t,u(t))|, L=\max_{t_0 \le t \le T}|\frac{\partial f(t,u(t))}{\partial u}|, K=\max_{t_0 \le t \le T}|\frac{\partial f(t,u(t))}{\partial t}|.

例 2 取 $h=\frac{1}{16}$ , 用(2)式估计 Euler 方法求常微分方程初值问题

\left\{ \begin{aligned} &u'=u-\frac{2t}{u},0<t\le1 \\ &u_0=1, \end{aligned} \right.

的数值解 $u_m$ 与真解 $u(t_m)$ 的误差，并求实际误差相对照。

解：经过简单计算可得 $L=3,K=5,M_1=1$ , 所以

|\varepsilon_m| \le \frac{K+LM_1}{2L}[(1+hL)^m-1]h\\ =\frac{1}{12}[(1+\frac{3}{16})^m-1], m=1,2,\dots,16.

同样的，我们做了这些实验得到以下结果：

单步方法​

Euler 法​

算例 1​

多步法​

显式方法和隐式方法​

先验误差​

单步方法

Euler 法

算例 1

多步法

显式方法和隐式方法

先验误差